
【题目】在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上一动点,点Q为边AC上一动点,且∠PDQ=90°.

(1)求ED、EC的长;
(2)若BP=2,求CQ的长;
(3)记线段PQ与线段DE的交点为点F,若△PDF为等腰三角形,求BP的长.
【答案】(1)![]() ,
,![]() ;(2)CQ
;(2)CQ![]() 或CQ
或CQ![]() ;(3)
;(3)![]() 或
或![]()
【解析】
试题分析:(1)先根据勾股定理求得BC的长,再结合点D为BC的中点可得CD的长,然后证得△ABC∽△DEC,根据相似三角形的性质即可求得结果;
(2)分①当点P在AB边上时,②当点P在AB的延长线上时,根据相似三角形的性质求解即可;
(3)由△BPD∽△EQD可得![]() ,若设BP=x ,则
,若设BP=x ,则![]() ,
,![]() ,可得
,可得![]() ,即得∠QPD=∠C,又可证∠PDE=∠CDQ,则可得△PDF∽△CDQ,再分①当CQ=CD时,②当QC=QD时,③当DC=DQ时,三种情况,根据等腰三角形的性质求解即可.
,即得∠QPD=∠C,又可证∠PDE=∠CDQ,则可得△PDF∽△CDQ,再分①当CQ=CD时,②当QC=QD时,③当DC=DQ时,三种情况,根据等腰三角形的性质求解即可.
(1)在Rt△ABC中,∠A=90°,AB=6,AC=8
∴BC=10
点D为BC的中点
∴CD=5
可证△ABC∽△DEC
∴![]() , 即
, 即![]()
∴![]() ,
,![]() ;
;
(2)①当点P在AB边上时,在Rt△ABC中,∠B+∠C=90°,
在Rt△EDC中,∠DEC+∠C=90°,
∴∠DEC=∠B
∵DE⊥BC,∠PDQ=90°
∴∠PDQ=∠BDE=90°
∴∠BDP=∠EDQ
∴△BPD∽△EQD
∴![]() ,即
,即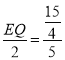 ,
,
∴![]()
∴CQ=EC-EQ![]() ;
;
②当点P在AB的延长线上时,同理可得:![]() ,
,
∴CQ=EC+EQ![]() ;
;
(3)∵线段PQ与线段DE的交点为点F,
∴点P在边AB上
∵△BPD∽△EQD
∴![]()
若设BP=x ,则![]() ,
,![]() ,可得
,可得![]()
∴∠QPD=∠C
又可证∠PDE=∠CDQ
∴△PDF∽△CDQ
∵△PDF为等腰三角形
∴△CDQ为等腰三角形
①当CQ=CD时,可得![]() ,解得
,解得![]()
②当QC=QD时, 过点Q作QM⊥CB于M,
∴![]() ,
,![]()
∴![]() ,解得
,解得![]()
③当DC=DQ时,过点D作DN⊥CQ于N,
∴![]() ,
,![]()
∴![]() ,解得
,解得![]() (不合题意,舍去)
(不合题意,舍去)
∴综上所述,![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
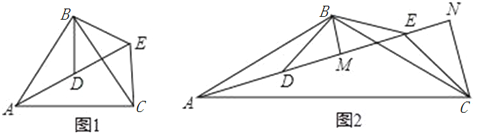
【题目】如图,△ABC和△DBE均为等腰三角形,点A,D,E在同一直线上,连接CE.
(1)如图1,若∠BAC=∠BCA=∠BDE=∠BED=55°
①求证:AD=CE;
②求∠AEC的度数.
(2)如图2,若∠ABC=∠DBE=120°,BM为△BDE中DE边上的高,CN为△ACE中AE边上的高,![]() 试证明:AE=
试证明:AE=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个水池,其底面是边长为16尺的正方形,一根芦苇AB生长在它的正中央,高出水面部分BC的长为2尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B′,则这根芦苇AB的长是( )
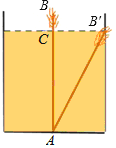
A. 15尺B. 16尺C. 17尺D. 18尺
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了了解学生每周在校参加体育锻炼的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:


(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某专业户要出售300只羊,现在市场上羊的价格为每千克11元,为了估计这300只羊能卖多少钱,试问:
(1)对于上述问题你认为适用___________.(填“普查”或“抽样调查”)
(2)该专业户从口随机抽取了5只羊,称得它们的质量(单位:千克)如下:26,31,32 ,36,37
①在这个问题中,总体、个体和样本各是___________,___________,___________.
②通过上述数据,你能估算出这300只羊能卖多少钱吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C在一条直线上,![]() ,
,![]() 均为等边三角形,连接AE、CD.AE分别交CD、BD于点M.P.CD交BE于点Q.
均为等边三角形,连接AE、CD.AE分别交CD、BD于点M.P.CD交BE于点Q.
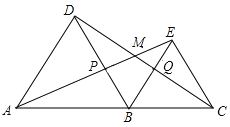
求证:(1)![]() ;
;
(2)连接MB,MB平分![]() 吗?并说明理由.
吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a是不为1的有理数,我们把![]() 称为a的差倒数,如2的差倒数是
称为a的差倒数,如2的差倒数是![]() =-1.现已知a1=
=-1.现已知a1=![]() ,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数.
,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数.
(1)求a2,a3,a4的值.
(2)根据(1)的计算结果,请猜想并写出a2018·a2019·a2020的值.
(3)计算:a1+a2+a3+…+a2018+a2019.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移一个单位”为一次变换.如此这样,连续经过2018次变换后,正方形ABCD的对角线交点M的坐标为( )
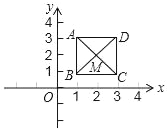
A. (2018,2) B. (2018,﹣2) C. (﹣2016,2) D. (2016,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:![]() 是关于
是关于 ![]() ,
,![]() 的多项式,如果
的多项式,如果 ![]() ,那么
,那么 ![]() 叫做“对称多项式”.例如,如果
叫做“对称多项式”.例如,如果 ![]() ,则
,则 ![]() 显然 ,所以
显然 ,所以 ![]() 是“对称多项式”.
是“对称多项式”.
(1)![]() 是“对称多项式”,试说明理由;
是“对称多项式”,试说明理由;
(2)请写一个“对称多项式”,![]() (不多于四项);
(不多于四项);
(3)如果 ![]() 和
和 ![]() 均为“对称多项式”,那么
均为“对称多项式”,那么 ![]() 一定是“对称多项式”吗?如果一定,请说明理由,如果不一定,请举例说明.
一定是“对称多项式”吗?如果一定,请说明理由,如果不一定,请举例说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com