
【题目】某专业户要出售300只羊,现在市场上羊的价格为每千克11元,为了估计这300只羊能卖多少钱,试问:
(1)对于上述问题你认为适用___________.(填“普查”或“抽样调查”)
(2)该专业户从口随机抽取了5只羊,称得它们的质量(单位:千克)如下:26,31,32 ,36,37
①在这个问题中,总体、个体和样本各是___________,___________,___________.
②通过上述数据,你能估算出这300只羊能卖多少钱吗?
【答案】(1)抽样调查;(2)①300只羊的质量,每只羊的质量,所抽取的5只羊的质量;②这300只羊能卖106920元
【解析】
(1)因为羊的头数太多,不宜采用全面调查方式去调查,应先用省时省力的方式采用抽样调查;
(2)①根据总体、个体、样本的定义回答即可;
②先求出样本平均数再估计300只羊每只羊的平均重量;再用300只羊的平均重量乘以300再乘以价格可得这300只羊卖的钱数.
(1)因为羊的头数太多,不宜采用全面调查方式去调查,应先用省时省力的方式采用抽样调查;
故答案为:抽样调查
(2)由题意可知,总体是300羊的质量;个体是每只羊的质量;样本是所抽取的5只羊的质量;
故答案为:300只羊的质量,每只羊的质量,所抽取的5只羊的质量
②![]() (千克),
(千克),
![]() (元).
(元).
即估计这300只羊能卖106920元.


科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.

(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠DPF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】命题:有两个角相等的三角形是等腰三角形(简称“等角对等边”).
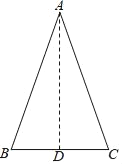
已知:如图,△ABC中,∠B=∠C.
求证:AB=AC.
三位同学作出了三种不同的辅助线,并完成了命题的证明.小刚的方法:作∠BAC的平分线AD,可证△ABD≌△ACD,得AB=AC;小亮的方法:作BC边上的高AD,可证△ABD≌△ACD,得AB=AC;小莉的方法:作BC边上的中线AD.
(1)请你写出小刚与小亮方法中△ABD≌△ACD的理由:
(2)请你按照小莉的思路完成命题的证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,D为AB边上一点,连接CD,E为CD的中点,连接BE并延长至点F,使得EF=EB,连接DF交AC于点G,连接CF,
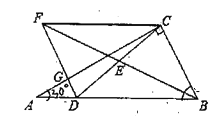
(1)求证:四边形DBCF是平行四边形
(2)若∠A=30°,BC=4,CF=6,求CD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B两地在数轴上相距20米,A地在数轴上表示的点为-8,小乌龟从A地出发沿数轴往B地方向前进,第一次前进1米,第二次后退2米,第三次再前进3米,第四次又后退4米,……,按此规律行进,(数轴的一个单位长度等于1米)
![]()
(1)求B地在数轴上表示的数;
(2)若B地在原点的左侧,经过第五次行进后小乌龟到达点P,第六次行进后到达点Q,则点P和点Q到点A的距离相等吗?请说明理由;
(3)若B地在原点的右侧,那么经过30次行进后,小乌龟到达的点与点B之间的距离是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上一动点,点Q为边AC上一动点,且∠PDQ=90°.

(1)求ED、EC的长;
(2)若BP=2,求CQ的长;
(3)记线段PQ与线段DE的交点为点F,若△PDF为等腰三角形,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解家长关注孩子成长方面的状况,学校开展了针对学生家长的“您最关心孩子哪方面成长”的主题调查,调查设置了“健康安全”、“日常学习”、“习惯养成”、“情感品质”四个项目,并随机抽取甲、乙两班共100位学生家长进行调查,根据调查结果,绘制了如图不完整的条形统计图.
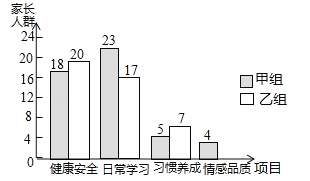
(1)补全条形统计图.
(2)若全校共有3600位学生家长,据此估计,有多少位家长最关心孩子“情感品质”方面的成长?
(3)综合以上主题调查结果,结合自身现状,你更希望得到以上四个项目中哪方面的关注和指导?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
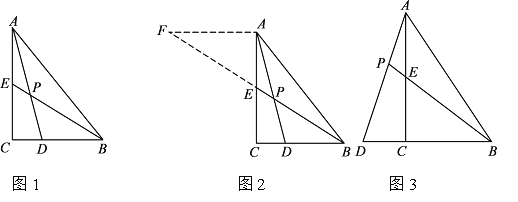
小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求![]() 的值.
的值.
小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).请回答:![]() 的值为 .
的值为 .
参考小昊思考问题的方法,解决问题:
如图 3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
(1)求![]() 的值;
的值;
(2)若CD=2,则BP=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题:

(1)一个水瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,另外购买的水杯按原价卖.若某单位想要买5个水瓶和20个水杯,请问选择哪家商场购买更合算,并说明理由.(必须在同一家购买)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com