
科目: 来源: 题型:
【题目】在长方形ABCD中,AB=a,BC=2a,点P在边BA上,点Q在边CD上,且BP=m,CQ=n,其中,m<a,n<a,m≠n,在长方形ABCD中,分别以BP、CQ为边作正方形BPP1P2,正方形CQQ1Q2(点P2、Q2在边BC上).
(1)画出图形.

(2)当m<n时,求三角形PQ1C的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大.
其中正确的结论有( )
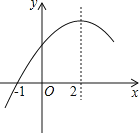
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】在长方形![]() 中,
中,![]() 厘米,
厘米,![]() 厘米,点
厘米,点![]() 沿
沿![]() 边从点
边从点![]() 开始向终点
开始向终点![]() 以2厘米/秒的速度移动;点
以2厘米/秒的速度移动;点![]() 沿
沿![]() 边从点
边从点![]() 开始向终点
开始向终点![]() 以1厘米/秒的速度移动.如果
以1厘米/秒的速度移动.如果![]() 、
、![]() 同时出发,用
同时出发,用![]() (秒)表示移动的时间.试解决下列问题:
(秒)表示移动的时间.试解决下列问题:
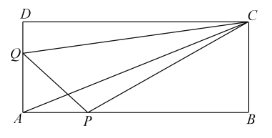
(1)用含有![]() 、
、![]() 的代数式表示三角形
的代数式表示三角形![]() 的面积;
的面积;
(2)求三角形![]() 的面积(用含有
的面积(用含有![]() 、
、![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目: 来源: 题型:
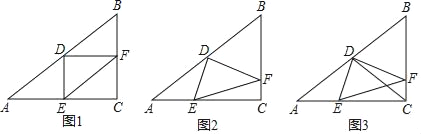
【题目】如图,已知△ABC中,∠ACB=90°,AC=8,cosA=![]() ,D是AB边的中点,E是AC边上一点,联结DE,过点D作DF⊥DE交BC边于点F,联结EF.
,D是AB边的中点,E是AC边上一点,联结DE,过点D作DF⊥DE交BC边于点F,联结EF.
(1)如图1,当DE⊥AC时,求EF的长;
(2)如图2,当点E在AC边上移动时,∠DFE的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出∠DFE的正切值;
(3)如图3,联结CD交EF于点Q,当△CQF是等腰三角形时,请直接写出BF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】为治理污水,甲乙两区都需要各自铺设一段污水排放管道。甲乙两区八月份都各铺了![]() 米,在九月份和十月份中,甲区的工作量平均每月增长
米,在九月份和十月份中,甲区的工作量平均每月增长![]() ,乙区则平均每月减少
,乙区则平均每月减少![]() 。
。
(1)九月份甲铺设了____________米排污管,乙铺设了_____________米排污管;(用含字母![]() 的代数式表示)
的代数式表示)
(2)如果![]() 且
且![]() ,那么十月份甲区比乙区多铺多少米排污管?
,那么十月份甲区比乙区多铺多少米排污管?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:b是最小的正整数,且a、b满足![]() +
+![]() =0,请回答问题:
=0,请回答问题:
(1)请直接写出a、b、c的值;
(2)数轴上a、b、c所对应的点分别为A、B、C,点M是A、B之间的一个动点,其对应的数为m,请化简![]() (请写出化简过程);
(请写出化简过程);
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动.若点A以每秒1个单位长度的速度向左运动.同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动.假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC-AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
科目: 来源: 题型:
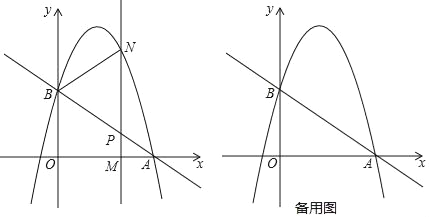
【题目】如图,抛物线y=﹣![]() +bx+c过点A(3,0),B(0,2).M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
+bx+c过点A(3,0),B(0,2).M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
(1)求直线AB的解析式和抛物线的解析式;
(2)如果点P是MN的中点,那么求此时点N的坐标;
(3)如果以B,P,N为顶点的三角形与△APM相似,求点M的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】数学是一门充满乐趣的学科,某校七年级小凯同学的数学学习小组遇到一个富有挑战性的探宄问题,请你帮助他们完成整个探究过程;
(问题背景)
对于一个正整数n,我们进行如下操作:
(1)将n拆分为两个正整数m1,m2的和,并计算乘积m1×m2;
(2)对于正整数m1,m2,分别重复此操作,得到另外两个乘积;
(3)重复上述过程,直至不能再拆分为止,(即折分到正整数1);
(4)将所有的乘积求和,并将所得的数值称为该正整数的“神秘值”,
请探究不同的拆分方式是否影响正整数n的“神秘值”,并说明理由.
(尝试探究):

(1)正整数1和2的“神秘值”分别是
(2)为了研究一般的规律,小凯所在学习小组通过讨论,决定再选择两个具体的正整数6和7,重复上述过程
探究结论:
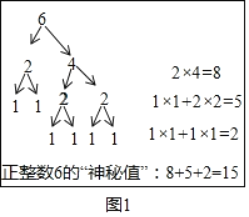
如图所示,是小凯选择的一种拆分方式,通过该拆分方法得到正整数6的“神秘值”为15.
请模仿小凯的计算方式,在如图中,选择另外一种拆分方式,给出计算正整数6的“神秘值”的过程;对于正整数7,请选择一种拆分方式,在如图中绐出计算正整数7的“神秘值”的过程.
(结论猜想)
结合上面的实践活动,进行更多的尝试后,小凯所在学习小组猜测,正整数n的“神秘值”与其折分方法无关.请帮助小凯,利用尝试成果,猜想正整数n的“神秘值”的表达式为 ,(用含字母n的代数式表示,直接写出结果)
查看答案和解析>>
科目: 来源: 题型:
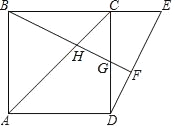
【题目】如图,点E是正方形ABCD的边BC延长线上一点,联结DE,过顶点B作BF⊥DE,垂足为F,BF交边DC于点G.
(1)求证:GDAB=DFBG;
(2)联结CF,求证:∠CFB=45°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com