
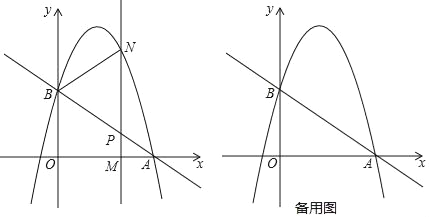
【题目】如图,抛物线y=﹣![]() +bx+c过点A(3,0),B(0,2).M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
+bx+c过点A(3,0),B(0,2).M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
(1)求直线AB的解析式和抛物线的解析式;
(2)如果点P是MN的中点,那么求此时点N的坐标;
(3)如果以B,P,N为顶点的三角形与△APM相似,求点M的坐标.
【答案】(1)直线AB的解析式为y=﹣![]() x+2,抛物线解析式为y=﹣
x+2,抛物线解析式为y=﹣![]() x2+
x2+![]() x+2;(2)N点坐标为(
x+2;(2)N点坐标为(![]() ,
, ![]() );(3)点M的坐标为(
);(3)点M的坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】试题分析:(1)运用待定系数法求解即可;
(2设N(m,﹣ ![]() m2+
m2+![]() m+2),P(m,﹣
m+2),P(m,﹣![]() m+2),那么NP=﹣
m+2),那么NP=﹣![]() m2+4m,PM=﹣
m2+4m,PM=﹣![]() m+2,根据NP=PM列方程求解即可;
m+2,根据NP=PM列方程求解即可;
(3)分△BPN∽△OBA和△BPN∽△ABO两种情况,列方程求解.
解:(1)设直线AB的解析式为y=px+q,
把A(3,0),B(0,2)代入得![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为y=﹣![]() x+2;
x+2;
把A(3,0),B(0,2)代入y=﹣![]() +bx+c得
+bx+c得 ,解得
,解得![]() ,
,
∴抛物线解析式为y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)∵M(m,0),MN⊥x轴,
∴N(m,﹣![]() m2+
m2+![]() m+2),P(m,﹣
m+2),P(m,﹣![]() m+2),
m+2),
∴NP=﹣![]() m2+4m,PM=﹣
m2+4m,PM=﹣![]() m+2,
m+2,
而NP=PM,
∴﹣![]() m2+4m=﹣
m2+4m=﹣![]() m+2,解得m1=3(舍去),m2=
m+2,解得m1=3(舍去),m2=![]() ,
,
∴N点坐标为(![]() ,
,![]() );
);
(3)∵A(3,0),B(0,2),P(m,﹣![]() m+2),
m+2),
∴AB=![]() =
=![]() ,BP=
,BP=![]() =
=![]() m,
m,
而NP=﹣![]() m2+4m,
m2+4m,
∵MN∥OB,
∴∠BPN=∠ABO,
当![]() =
=![]() 时,△BPN∽△OBA,则△BPN∽△MPA,即
时,△BPN∽△OBA,则△BPN∽△MPA,即![]() m:2=(﹣
m:2=(﹣![]() m2+4m):
m2+4m):![]() ,
,
整理得8m2﹣11m=0,解得m1=0(舍去),m2=![]() ,
,
此时M点的坐标为(![]() ,0);
,0);
当![]() =
=![]() 时,△BPN∽△ABO,则△BPN∽△APM,即
时,△BPN∽△ABO,则△BPN∽△APM,即![]() m:
m:![]() =(﹣
=(﹣![]() m2+4m):2,
m2+4m):2,
整理得2m2﹣5m=0,解得m1=0(舍去),m2=![]() ,
,
此时M点的坐标为(![]() ,0);
,0);
综上所述,点M的坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点E、F分别是AB、CD上的点,点G是BC的延长线上一点,且∠B=∠DCG=∠D 则下列判断错误的是( )
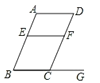
A.∠BEF=∠EFDB.∠A=∠BCFC.∠AEF=∠EBCD.∠BEF+∠EFC=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在互联网技术的影响下,幸福新村的村民小刘在网上销售苹果,原计划每天卖100千克,但实际每天的销量与计划销量相比有出入,如表是某周的销售情况(超额记为正,不足记为负.单位:千克):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 |
|
|
|
|
|
|
|
(1)根据表中的数据可知前三天共卖出___________千克;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售多少千克?
(3)若每千克按5元出售,每千克苹果的运费为1元,那么小刘本周一共收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠A=30°,BC=2,CD是斜边AB上的高,点E为边AC上一点(点E不与点A、C重合),联结DE,作CF⊥DE,CF与边AB、线段DE分别交于点F、G;
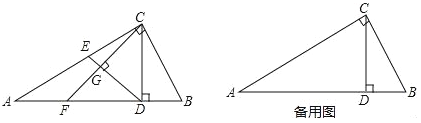
(1)求线段CD、AD的长;
(2)设CE=x,DF=y,求y关于x的函数解析式,并写出它的定义域;
(3)联结EF,当△EFG与△CDG相似时,求线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有三个点A、B、C,表示的数分别是-4、-2、3,请回答:
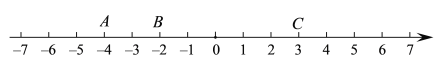
(1)若C、B两点的距离与A、B两点距离相等,则需将点C向左移动________个单位;
(2)若移动A、B、C三点中的两点,使三个点表示的数相同,移动方法有________种,其中移动所走的距离之和最小的是________个单位;
(3)若在B处有一小青蛙,一步跳一个单位长,小青蛙第一次先向左跳一步,第2次向右跳3步,第3次向再向左跳5步,第4次再向右跳7步……,按此规律继续下去,那么跳第100次时落脚点表示的数是________;
(4)若有两只小青蛙M、N,它们在数轴上的点表示的数分别为整数x、y,且|x-2|+|y+3|=2,求两只青蛙M、N之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大.
其中正确的结论有( )
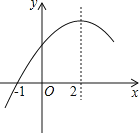
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点,已知一次函数y=kx+b的图象上的点A(1,0)及B.
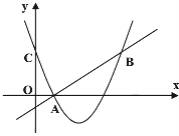
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足kx+b≤(x-2)2+m的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某巡警骑摩托车在一条东西直大道上巡逻,某天他从岗亭出发,晚上停留在A处,规定向东方向为正,当天行驶情况记录如下(单位:千米):
+9, -5, +7, -14, +1, -10, +8;
(1)点A在岗亭的 边方向,距离岗亭 千米。
(2)若他离开岗亭超过10千米对讲机就会与岗亭值班员失联,请问他这一天有没有失联过?有几次?请说明理由。
(3)若摩托车每行驶100千米耗油6升,这一天共耗油多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com