
科目: 来源: 题型:
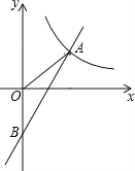
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求一次函数y=kx+b和y=![]() 的表达式;
的表达式;
(2)已知点C在x轴上,且△ABC的面积是8,求此时点C的坐标;
(3)反比例函数y=![]() (1≤x≤4)的图象记为曲线C1,将C1向右平移3个单位长度,得曲线C2,则C1平移至C2处所扫过的面积是_________.(直接写出答案)
(1≤x≤4)的图象记为曲线C1,将C1向右平移3个单位长度,得曲线C2,则C1平移至C2处所扫过的面积是_________.(直接写出答案)
查看答案和解析>>
科目: 来源: 题型:
【题目】观察理解,并解决问题.
问题情境:如图所示,用一些相同的小正方形,拼在一起,排成如下的一些大正方形:
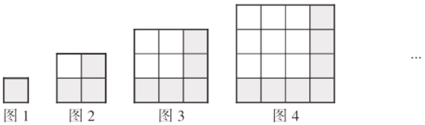
问题解决:(1)完成下表:
图序号 | 1 | 2 | 3 | 4 | … |
|
每一行小正方形的个数 | 1 | 2 | 3 | ______ | … | ______ |
阴影小正方形的个数 | 1 | 3 | 5 | ______ | … | ______ |
(2)根据图形规律推测:![]() ______(用含
______(用含![]() 的代数式表示)
的代数式表示)
(3)像(1),(2)这样,根据某类事物的部分对象具有的某种性质,推出这类事物的所有对象具有的这种性质的推理,叫做归纳推理.对于科学的发现,归纳推理是十分有用的,通过观察、实验,对有限个对象的性质作归纳整理,提出对某类事物带有规律性的猜测,是科学研究的基本方法.请观察下列等式的规律:第一个等式:![]() ;第二个等式:
;第二个等式:![]() ;第三个等式:
;第三个等式:![]() ;…猜想并直接写出第
;…猜想并直接写出第![]() 个等式.(用含
个等式.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一个长方形运动场被分隔成![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 共
共![]() 个区,
个区, ![]() 区是边长为
区是边长为![]() 的正方形,
的正方形, ![]() 区是边长为
区是边长为![]() 的正方形.
的正方形.
(1)列式表示每个![]() 区长方形场地的周长,并将式子化简;
区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果![]() ,
, ![]() ,求整个长方形运动场的面积.
,求整个长方形运动场的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外完全相同,其中红球有![]() 个,若从中随机摸出一个球,这个球是白球的概率为
个,若从中随机摸出一个球,这个球是白球的概率为![]() .
.
(![]() )请直接写出袋子中白球的个数.
)请直接写出袋子中白球的个数.
(![]() )随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
查看答案和解析>>
科目: 来源: 题型:
【题目】大熊山某农家乐为了抓住“五一”小长假的商机,决定购进A、B两种纪念品。若购进A种纪念品4件,B种纪念品3件,需要550元;若购进A种纪念品8件,B种纪念品5件,需要1050元。
(1)求购进A、B两种纪念品每件各需多少元。
(2)若该农家乐决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该农家乐共有几种进货方案。
(3)若销售每件A种纪念品可获利润30元,每件B种纪念品可获利润20元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元。
查看答案和解析>>
科目: 来源: 题型:
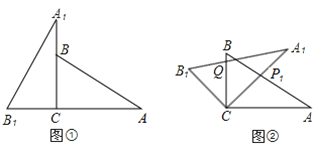
【题目】将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.
(1)将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;
(2)在图②中,若AP1=2,则CQ等于多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/公里计算,耗时费按y元/分钟计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与打车时间如表:
时间(分钟) | 里程数(公里) | 车费(元) | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
(1)求x,y的值;
(2)如果小华也用该打车方式,打车行驶了11公里,用了14分钟,那么小华的打车总费用为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】某居民小区的一处圆柱形的输水管道破裂,维修人员为更换管道,需要确定管道圆形截面的半径.如图,若这个输水管道有水部分的水面宽AB=16cm,水最深的地方的高度为4cm,求这个圆形截面的半径.
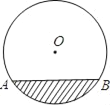
查看答案和解析>>
科目: 来源: 题型:
【题目】电子跳蚤游戏盘是如图所示的△ABC,AB=AC=BC=5.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1= CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2= AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3= BP2;…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2016与点P2017之间的距离为_________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com