
科目: 来源: 题型:
【题目】某商场对一种新售的手机进行市场问卷调查,其中一个项目是让每个人按A(不喜欢)、B(一般)、C(不比较喜欢)、D(非常喜欢)四个等级对该手机进行评价,图①和图②是该商场采集数据后,绘制的两幅不完整的统计图,请你根据以上统计图提供的信息,回答下列问题:
(1)本次调查的人数为多少人?A等级的人数是多少?请在图中补全条形统计图.
(2)图①中,a等于多少?D等级所占的圆心角为多少度?

查看答案和解析>>
科目: 来源: 题型:
【题目】已知y+1与x+2成正比例,且当x=4时,y=-4.
(1)求y关于x的函数关系式;
(2)若点(a,2)和(2,b)均在(1)中函数图像上,求a、b的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
(1)填空:a= ,b= ,c= ;
(2)先化简,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)]+4abc.

查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两辆摩托车同时从相距20km的A,B两地出发,相向而行.图中l1,l2分别表示甲、乙两辆摩托车到A地的距离s(km)与行驶时间t(h)的函数关系.则下列说法错误的是
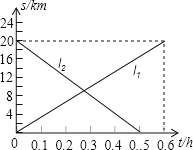
A. 乙摩托车的速度较快
B. 经过0.3小时甲摩托车行驶到A,B两地的中点
C. 经过0.25小时两摩托车相遇
D. 当乙摩托车到达A地时,甲摩托车距离A地![]() km
km
查看答案和解析>>
科目: 来源: 题型:
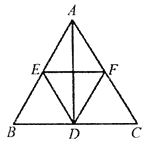
【题目】在![]() 中,D,E,F分别是三边
中,D,E,F分别是三边![]() ,
,![]() ,
,![]() 上的中点,连接
上的中点,连接![]() ,
,![]() ,
,![]() ,
,![]() ,已知
,已知![]() .
.
(1)观察猜想:如图,当![]() 时,①四边形
时,①四边形![]() 的对角线
的对角线![]() 与
与![]() 的数量关系是________;②四边形
的数量关系是________;②四边形![]() 的形状是_______;
的形状是_______;

(2)数学思考:如图,当![]() 时,(1)中的结论①,②是否发生变化?若发生变化,请说明理由;
时,(1)中的结论①,②是否发生变化?若发生变化,请说明理由;
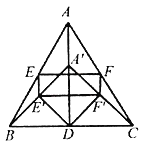
(3)拓展延伸:如图,将上图的点A沿![]() 向下平移到
向下平移到![]() 点,使得
点,使得![]() ,已知
,已知![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,求四边形
的中点,求四边形![]() 与四边形
与四边形![]() 的面积比.
的面积比.
查看答案和解析>>
科目: 来源: 题型:
【题目】某花卉基地出售文竹和发财树两种盆栽,其单价为:文竹盆栽12元/盆,发财树盆栽15元/盆。如果同一客户所购文竹盆栽的数量大于800盆,那么每盆文竹可降价2元.某花卉销售店向花卉基地采购文竹400盆~900盆,发财树若干盆,此销售店本次用于采购文竹和发财树恰好花去12000元.然后再以文竹15元,发财树20元的单价实卖出.若设采购文竹x盆,发财树y盆,毛利润为W元.

(1)当![]() 时,y与x的数量关系是_______,W与x的函数解析式是_________;
时,y与x的数量关系是_______,W与x的函数解析式是_________;
当![]() 时,y与x的数量关系是___________,W与x的函数解析式是________;
时,y与x的数量关系是___________,W与x的函数解析式是________;
(2)此花卉销售店应如何采购这两种盆栽才能使获得毛利润最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形![]() 两顶点为
两顶点为![]() ,
,![]() ,点D的坐标为
,点D的坐标为![]() ,在
,在![]() 上取点E,使得
上取点E,使得![]() ,连接
,连接![]() ,分别交
,分别交![]() ,
,![]() 于M,N两点.
于M,N两点.
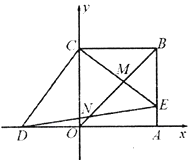
(1)求证:![]() ;
;
(2)求点E的坐标和线段![]() 所在直线的解析式;
所在直线的解析式;
(3)在M,N两点中任选一点求出它的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.
(1)四棱柱有 个面, 条棱, 个顶点;
(2)六棱柱有 个面, 条棱, 个顶点;
(3)由此猜想n棱柱有 个面, 条棱, 个顶点.

查看答案和解析>>
科目: 来源: 题型:
【题目】某中学八年级举行跳绳比赛,要求每班选出5名学生参加,在规定时间每人跳绳不低于150次为优秀,冠、亚军在八(1)、八(5)两班中产生.下表是这两个班的5名学生的比赛数据(单位:次)
1号 | 2号 | 3号 | 4号 | 5号 | 平均数 | 方差 | |
八(1)班 | 139 | 148 | 150 | 160 | 153 | 150 | 46.8 |
八(5)班 | 150 | 139 | 145 | 147 | 169 | 150 | 103.2 |
根据以上信息,解答下列问题:
(1)求两班的优秀率及两班数据的中位数;
(2)请你从优秀率、中位数和方差三方面进行简要分析,确定获冠军奖的班级.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com