
科目: 来源: 题型:
【题目】如图,已知E、F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM=![]() MF.其中正确结论的个数是( )
MF.其中正确结论的个数是( )
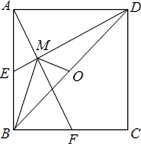
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,已知抛物线![]() 与y轴交于点A(0,﹣4),与x轴相交于B(﹣2,0)、C(4,0)两点,O为坐标原点.
与y轴交于点A(0,﹣4),与x轴相交于B(﹣2,0)、C(4,0)两点,O为坐标原点.
(1)求抛物线的解析式;
(2)设点E在x轴上,∠OEA+∠OAB=∠ACB,求BE的长;
(3)如图2,将抛物线y=ax2+bx+c向右平移n(n>0)个单位得到的新抛物线与x轴交于M、N(M在N左侧),P为x轴下方的新抛物线上任意一点,连PM、PN,过P作PQ⊥MN于Q,![]() 是否为定值?请说明理由.
是否为定值?请说明理由.
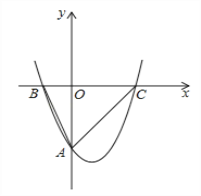
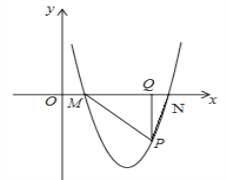
图1 图2
查看答案和解析>>
科目: 来源: 题型:
【题目】开学初,小芳和小亮去学校商店购买学习用品,小芳用18元钱买了1支钢笔和3本笔记本,小亮用31元买了同样的钢笔2支和笔记本5本.
(1)求每支钢笔和每本笔记本的价格;
(2)校运会后,班主任拿出200元学校奖励基金交给班长,购买上述价格的钢笔和笔记本共48件作为奖品,奖给校运会表现突出的同学,要求笔记本数不少于钢笔数.请问:有多少购买方案?请你一一写出.
查看答案和解析>>
科目: 来源: 题型:
【题目】从三角形一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的优美线.
(1)如图,在△ABC中,AD为角平分线,∠B=50°,∠C=30°,求证:AD为△ABC的优美线;
(2)在△ABC中,∠B=46°,AD是△ABC的优美线,且△ABD是以AB为腰的等腰三角形,求∠BAC的度数;
(3)在△ABC中,AB=4,AC=2,AD是△ABC的优美线,且△ABD是等腰三角形,直接写出优美线AD的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】“春节”是我国的传统佳节,民间历来有吃“汤圆”的习俗。某食品厂为了了解市民对去年销量较好的肉馅(A)、豆沙馅(B)、菜馅(C)、三丁馅(D)四种不同口味汤圆的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整)。请根据以上信息回答:
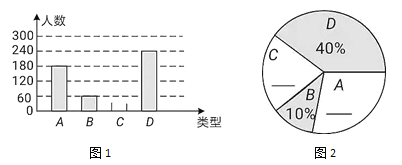
(1)从全体学生的调查表中随机抽取了多少名学生?
(2)将图1和图2补充完整;
(3)图2中表示“A”的圆心角是多少度?
查看答案和解析>>
科目: 来源: 题型:
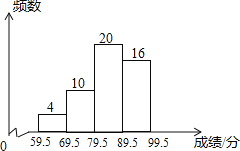
【题目】为增强学生环保意识,某中学组织全校3000名学生参加环保知识大赛,比赛成绩均为整数.从中抽取部分同学的成绩进行统计,并绘制成如下统计图.
请根据图中提供的信息,解答下列问题:
(1)若抽取的成绩用扇形图来描述,则表示“第二组(69.5~79.5)”的扇形的圆心角 度;
(2)若成绩在90分以上(含90分)的同学可获奖,请估计该校约有多少名同学获奖?
(3)某班准备从成绩最好的4名同学(男、女各2名)中随机选取2名同学去社区进行环保宣传,则选出的同学恰好是1男1女的概率为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com