
科目: 来源: 题型:
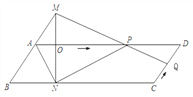
【题目】如图,已知□ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1),解答下列问题:
(1)是否存在时刻t,使点P在∠BCD的平分线上;
(2)设四边形ANPM的面积为S(cm),求S与t之间的函数关系式;
(3)是否存在某一时刻t,使四边形ANPM与□ABCD面积相等,若存在,求出相应的t值,若不存在,说明理由;
(4)求t为何值时,△ABN为等腰三角形.
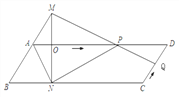
备用图
查看答案和解析>>
科目: 来源: 题型:
【题目】暑假期间,小明和父母一起开车到距家200千米的景点旅游.出发前,汽车油箱内储油45升;当行驶150千米时,发现油箱剩余油量为30升.
(1)已知油箱内余油量y(升)是行驶路程x(千米)的一次函数,求y与x的函数关系式;
(2)当油箱中余油量少于3升时,汽车将自动报警.如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)平面上有四个点A,B,C,D,按照以下要求作图:
①作直线AD;
②作射线CB交直线AD于点E;
③连接AC,BD交于点F;
(2)图中共有 条线段;
(3)若图中F是AC的一个三等分点,AF<FC,已知线段AC上所有线段之和为18,求AF长.
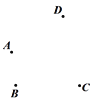
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知∠AOB=α°,∠COD在∠AOB内部且∠COD=β°.
(1)若α,β满足|α-2β|+(β-60)2=0,则①α= ;
②试通过计算说明∠AOD与∠COB有何特殊关系;
(2)在(1)的条件下,如果作OE平分∠BOC,请求出∠AOC与∠DOE的数量关系;
(3)若α°,β°互补,作∠AOC,∠DOB的平分线OM,ON,试判断OM与ON的位置关系,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】问题提出:某段楼梯共有10个台阶,如果某同学在上台阶时,可以一步1个台阶,也可以一步2个台阶.那么该同学从该段楼梯底部上到顶部共有多少种不同的走法?
问题探究:
为解决上述实际问题,我们先建立如下数学模型:
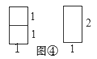
如图①,用若干个边长都为1的正方形(记为1×1矩形)和若干个边长分别为1和2的矩形(记为1×2矩形),要拼成一个如图②中边长分别为1和n的矩形(记为1×![]() 矩形),有多少种不同的拼法?(设
矩形),有多少种不同的拼法?(设![]() 表示不同拼法的个数)
表示不同拼法的个数)
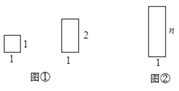
为解决上述数学模型问题,我们采取的策略和方法是:一般问题特殊化.
探究一:先从最特殊的情形入手,即要拼成一个1×1矩形,有多少种不同拼法?
显然,只有1种拼法,如图③,即![]() =1种.
=1种.
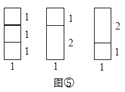
探究二:要拼成一个1×2矩形,有多少种不同拼法?
可以看出,有2种拼法,如图④,即![]() =2种.
=2种.
探究三:要拼成一个1×3矩形,有多少种不同拼法?
拼图方法可分为两类:一类是在图④这2种1×2矩形上方,各拼上一个1×1矩形,即这类拼法共有![]() =2种;另一类是在图③这1种1×1矩形上方拼上一个1×2矩形,即这类拼法有
=2种;另一类是在图③这1种1×1矩形上方拼上一个1×2矩形,即这类拼法有![]() =1种.如图⑤,即
=1种.如图⑤,即![]() =
=![]() +
+![]() = 2+1=3(种).
= 2+1=3(种).
![]()
探究四:仿照上述探究过程,要拼成一个1×4矩形,有多少种不同拼法?请画示意图说明并求出结果.
探究五:要拼成一个1×5矩形,仿照上述探究过程,得出![]() = 种不同拼法.
= 种不同拼法.
(直接写出结果,不需画图).
问题解决:请你根据上述中的数学模型,解答“问题提出”中的实际问题.
(写出解答过程,不需画图).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和
矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的
距离是11m,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
(1)求抛物线的解析式;
(2)已知从某时刻开始的40h内,水面与河底ED的距离h(单位:m)随时间t(单位:h)的变化满足函数
关系![]() 且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
查看答案和解析>>
科目: 来源: 题型:
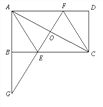
【题目】如图,在平行四边形ABCD中,点O是AC中点,AC=2AB,延长AB到G,使BG=AB,连接GO并延长,分别交BC于点E,交AD于点F.
(1)求证:△ABC≌△AOG;
(2)若ABCD为矩形,则四边形AECF是什么特殊四边形?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
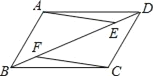
【题目】如图,在ABCD中,点E、F在BD上,且BF=DE.
(1)写出图中所有你认为全等的三角形;
(2)延长AE交BC的延长线于G,延长CF交DA的延长线于H(请补全图形),证明四边形AGCH是平行四边形.
查看答案和解析>>
科目: 来源: 题型:
【题目】仔细阅读下列材料.
“分数均可化为有限小数或无限循环小数”,反之,“有限小数或无限小数均可化为分数”.
例如:![]() =1÷4=0.25;
=1÷4=0.25;![]() =
=![]() =8÷5=1.6;
=8÷5=1.6;![]() =1÷3=
=1÷3=![]() ,反之,0.25=
,反之,0.25=![]() =
=![]() ;1.6=
;1.6=![]() =
=![]() =
=![]() .那么
.那么![]() ,
,![]() 怎么化成分数呢?
怎么化成分数呢?
解:∵![]() ×10=3+
×10=3+![]() , ∴不妨设
, ∴不妨设![]() =x,则上式变为10x=3+x,解得x=
=x,则上式变为10x=3+x,解得x=![]() ,即
,即![]() =
=![]() ;
;
∵![]() =
=![]() ,设
,设![]() =x,则上式变为100x=2+x,解得x=
=x,则上式变为100x=2+x,解得x=![]() ,
,
∴![]() =
=![]() =1+x=1+
=1+x=1+![]() =
=![]()
⑴将分数化为小数:![]() =______,
=______,![]() =_______;
=_______;
⑵将小数化为分数:![]() =______,
=______,![]() =_______;
=_______;
⑶将小数![]() 化为分数,需要写出推理过程.
化为分数,需要写出推理过程.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线L:y=3x+2,现有下列命题:
①过点P(-1,1)与直线L平行的直线是y=3x+4;②若直线L与x轴、y轴分别交于A、B两点,则AB=![]() ;③若点M(-
;③若点M(-![]() ,1),N(a,b)都在直线L上,且a>-
,1),N(a,b)都在直线L上,且a>-![]() ,则b>1; ④若点Q到两坐标轴的距离相等,且Q在L上,则点Q在第一或第二象限。其中正确的命题是_________.
,则b>1; ④若点Q到两坐标轴的距离相等,且Q在L上,则点Q在第一或第二象限。其中正确的命题是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com