
科目: 来源: 题型:
【题目】A、B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运30kg,A型机器人搬运900kg与B型机器人搬运600kg所用时间相等,两种机器人每小时分别搬运多少化工原料?
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司10名销售员,去年完成的销售额情况如表:
销售额(单位:万元) | 3 | 4 | 5 | 6 | 7 | 8 | 10 |
销售员人数(单位:人) | 1 | 3 | 2 | 1 | 1 | 1 | 1 |
(1)求销售额的平均数、众数、中位数;
(2)今年公司为了调动员工积极性,提高年销售额,准备采取超额有奖的措施,请根据(1)的结果,通过比较,合理确定今年每个销售员统一的销售额标准是多少万元?
查看答案和解析>>
科目: 来源: 题型:
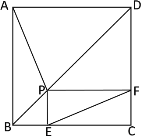
【题目】如图所示,点P是正方形ABCD的对角线BD上一点,PE⊥BC于E,PF⊥CD于F,连接EF,给出下列四个结论:①AP=EF;②△APD一定是等腰三角形;③∠PFE=∠BAP;④PD=![]() EC,其中正确结论的序号是_______.
EC,其中正确结论的序号是_______.
查看答案和解析>>
科目: 来源: 题型:
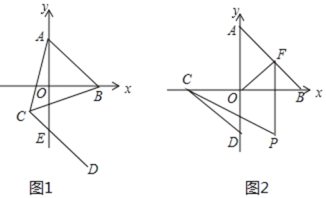
【题目】.如图 1,在平面直角坐标系中,A 、B 在坐标轴上,其中 A(0, a) ,B(b, 0)满足| a 3 |![]() 0.
0.
(1)求 A 、 B 两点的坐标;
(2)将 AB 平移到CD , A 点对应点C(2, m) , DE 交 y 轴于 E ,若ABC 的面积等于13,求点 E 的坐标;
(3)如图 2,若将 AB 平移到CD ,点 C、D 也在坐标轴上,F 为线段 AB 上一动点,(不包括点 A ,点B) ,连接OF 、FP 平分BFO ,BCP 2PCD,试探究COF,OFP ,CPF 的数量关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,⊙P的圆心是(2,a)(a >0),半径是2,与y轴相切于点C,直线y=x被⊙P截得的弦AB的长为![]() ,则a的值是( )
,则a的值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
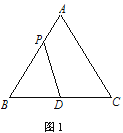
【题目】如图1,在等边△ABC中,D是BC的中点,P为AB 边上的一个动点,设AP=x,图1中线段DP的长为y,若表示y与x的函数关系的图象如图2所示,则△ABC的面积为( )
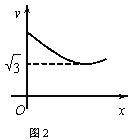
A. 4 B. ![]() C. 12 D.
C. 12 D. ![]()
查看答案和解析>>
科目: 来源: 题型:
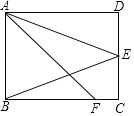
【题目】如图,在平行四边形ABCD中,点E是CD的中点,点F是BC边上的点,AF=AD+FC,平行四边形ABCD的面积为S,由A、E、F三点确定的圆的周长为t.
(1)若△ABE的面积为30,直接写出S的值;
(2)求证:AE平分∠DAF;
(3)若AE=BE,AB=4,AD=5,求t的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平行四边形ABCD中,点A1, A2, A3, A4和C1, C2, C3, C4分别是AB和CD的五等分点,点B1, B2和D1,D2分别是BC和DA的三等分点.已知四边形A4B2C4D2的面积为18,则平行四边形ABCD的面积为( )
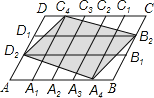
A. 22B. 25C. 30D. 15
查看答案和解析>>
科目: 来源: 题型:
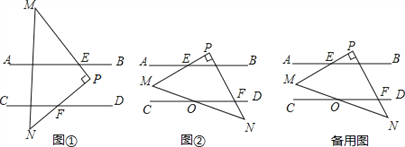
【题目】如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F
(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为 ;
(2)当△PMN所放位置如图②所示时,求证:∠PFD﹣∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com