
科目: 来源: 题型:
【题目】定义:如果三角形有一边上的中线长恰好等于这边的长,那么这个三角形叫“恰等三角形”,这条中线叫“恰等中线”.
(直角三角形中的“恰等中线”)
(1)如图1,在△ABC中,∠C=90°,AC=![]() ,BC=2,AM为△ABC的中线.求证:AM是“恰等中线”.
,BC=2,AM为△ABC的中线.求证:AM是“恰等中线”.

(等腰三角形中的“恰等中线”)
(2)已知,等腰△ABC是“恰等三角形”,AB=AC=20,求底边BC的平方.
(一般三角形中的“恰等中线”)
(3)如图2,若AM是△ABC的“恰等中线”,则BC2,AB2,AC2之间的数量关系为 .

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC是边长为6 cm的等边三角形,动点P从A出发,以3 cm/s的速度,沿A-B-C向C运动,同时,动点Q从C出发沿CA方向以1 cm/s的速度向A运动,当其中一点运动到终点时,两点同时停止运动.设运动时间为t秒,当t= ____s,△APQ是直角三角形.

查看答案和解析>>
科目: 来源: 题型:
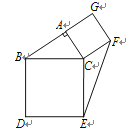
【题目】如图,在△ABC中,∠BAC=90°,分别以AC,BC为边长,在三角形外作正方形ACFG和正方形BCED.若AC=4,AB=6,则EF=______.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB=5,AC=4,∠B,∠C的平分线相交于点O,OM∥AB,ON∥AC分别与BC交于点M、N,则△OMN的周长为____.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 中,AB=AC,
中,AB=AC,![]() ,点D,E分别在AB,BC上,
,点D,E分别在AB,BC上,![]() ,点F为DE的延长线与AC的延长线的交点.
,点F为DE的延长线与AC的延长线的交点.
(1)求证:DE=EF
(2)判断BD和CF的数量关系,并说明理由;
(3)若![]() ,
,![]() ,求BD的长。
,求BD的长。

查看答案和解析>>
科目: 来源: 题型:
【题目】某小组做“频率具有稳定性”的试验时,绘出某一结果出现的频率折线图如图所示,则符合这一结果的试验可能是( )

A.抛一枚硬币,出现正面朝上
B.掷一个正六面体的骰子,掷出的点数是5
C.任意写一个整数,它能被2整除
D.从一个装有2个红球和1个白球的袋子中任取一球(这些球除颜色外完全相同),取到的是白球
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1所示,A、B两点同时从原点O出发,点A以每秒x个单位长度沿x轴的负方向运动,点B以每秒y个单位长度沿y轴的正方向运动.

(1)若|x+2y-10|+|2x-y|=0,试分别求出1秒钟后△AOB的面积;
(2)如图2,所示,设∠BAO的邻补角和∠ABO的邻补角的平分线相交于点P,问:点A、B在运动的过程中,∠P的大小是否会发生变化?若不发生变化,请求出其值;若发生变化,请说明理由;
(3)如图3所示,延长BA至E,在∠ABO的内部作射线BF交x轴于点C,若∠EAC、∠FCA、∠ABC的平分线相交于点G,过点G作BE的垂线,垂足为H,设∠AGH=α,∠BGC=β,试探究出α和β满足的数量关系并给出证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,∠A=40°,
(1)若点P是∠ABC与∠ACB平分线的交点,求∠P的度数;
(2)若点P是∠CBD与∠BCE平分线的交点,求∠P的度数;
(3)若点P是∠ABC与∠ACF平分线的交点,求∠P的度数;
(4)若∠A=β,求(1)(2)(3)中∠P的度数(用含β的代数式表示,直接写出结果)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com