
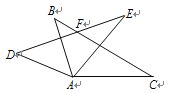
【题目】如图,△ABC≌△ADE,BC与DE交于点F.若∠BAE=60°,∠DAC=160°,则∠DFC的度数为____.
【答案】130°
【解析】
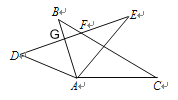
先根据全等三角形对应角相等求出∠BAC=∠DAE,所以∠BAD=∠CAE,然后求出∠BAD的度数,再根据∠B=∠D,∠AGD=∠FGB,可得∠DFB=∠BAD,然后可求∠DFC的度数.
解:∵△ABC≌△ADE,
∴∠BAC=∠DAE,∠B=∠D,
又∵∠BAD=∠DAE ∠BAE,∠CAE=∠BAC ∠BAE,
∴∠BAD=∠CAE,
∵∠DAC=160°,∠BAE=60°,
∴∠BAD=![]() (∠DAC∠BAE)=
(∠DAC∠BAE)=![]() (160°60°)=50°,
(160°60°)=50°,
∵∠B=∠D,∠AGD=∠FGB,
∴∠DFB=∠BAD=50°,
∴∠DFC=180°-50°=130°,
故答案为:130°.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
【题目】如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )

A. ![]() B. 2
B. 2![]() -
-![]() C. 2
C. 2![]() -
-![]() D. 4
D. 4![]() -
-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,![]() ,
,![]() ,点P是对角线AC上的动点
,点P是对角线AC上的动点![]() 不与点A,C重合
不与点A,C重合![]() ,连接PD,作
,连接PD,作![]() 交射线BC于点E,以线段PD,PE为邻边作矩形PEFD.
交射线BC于点E,以线段PD,PE为邻边作矩形PEFD.

![]() 线段PD的最小值为______;
线段PD的最小值为______;
![]() 求证:
求证:![]() ,并求矩形PEFD面积的最小值;
,并求矩形PEFD面积的最小值;
![]() 是否存在这样的点P,使得
是否存在这样的点P,使得![]() 是等腰三角形?若存在,请求出PE的长;若不存在,请说明理由.
是等腰三角形?若存在,请求出PE的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在长方形ABCD中,AB=8cm,BC=12cm,E为AB的中点,动点P在线段BC上以4cm/s的速度由点B向C运动,同时,动点Q在线段CD上由点C向点D运动,设运动时间为t(s).

(1)当t=2时,求△EBP的面积;
(2)若动点Q以与动点P不同的速度运动,经过多少秒,△EBP与△CQP全等?此时点Q的速度是多少?
(3)若动点Q以(2)中的速度从点C出发,动点P以原来的速度从点B同时出发,都逆时针沿长方形ABCD的四边形运动,经过多少秒,点P与点Q第一次在长方形ABCD的哪条边上相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为6 cm的等边三角形,动点P从A出发,以3 cm/s的速度,沿A-B-C向C运动,同时,动点Q从C出发沿CA方向以1 cm/s的速度向A运动,当其中一点运动到终点时,两点同时停止运动.设运动时间为t秒,当t= ____s,△APQ是直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区域为响应“绿水青山就是金山银山”的号召,加强了绿化建设.为了解该区域群众对绿化建设的满意程度,某中学数学兴趣小组在该区域的甲、乙两个片区进行了调查,得到如下不完整统计图.
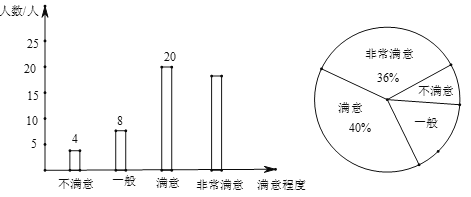
请结合图中信息,解决下列问题:
(1)此次调查中接受调查的人数为 人,其中“非常满意”的人数为 人;
(2)兴趣小组准备从“不满意”的4位群众中随机选择2位进行回访,已知这4位群众中有2位来自甲片区,另2位来自乙片区,请用画树状图或列表的方法求出选择的群众来自甲片区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用四个长为m,宽为n的相同长方形按如图方式拼成一个正方形.

(1).请用两种不同的方法表示图中阴影部分的面积.
方法①: ;
方法②: .
(2).由 (1)可得出![]() 2,
2,![]() ,4mn这三个代数式之间的一个等量关系为: .
,4mn这三个代数式之间的一个等量关系为: .
(3)利用(2)中得到的公式解决问题:已知2a+b=6,ab=4,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要720元;若购进甲种花卉40盆,乙种花卉30盆,需要880元.
(1)求购进甲、乙两种花卉,每盆各需多少元?
(2)该花店销售甲种花卉每盆可获利6元,销售乙种花卉每盆可获利1元,现该花店准备拿出800元全部用来购进这两种花卉,设购进甲种花卉x盆,全部销售后获得的利润为W元,求W与x之间的函数关系式;
(3)在(2)的条件下,考虑到顾客需求,要求购进乙种花卉的数量不少于甲种花卉数量的6倍,且不超过甲种花卉数量的8倍,那么该花店共有几种购进方案?在所有的购进方案中,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com