【题目】某区域为响应“绿水青山就是金山银山”的号召，加强了绿化建设.为了解该区域群众对绿化建设的满意程度，某中学数学兴趣小组在该区域的甲、乙两个片区进行了调查，得到如下不完整统计图.

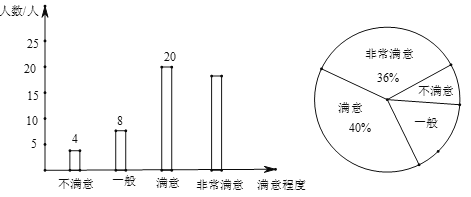
请结合图中信息，解决下列问题：

（1）此次调查中接受调查的人数为 人，其中“非常满意”的人数为 人；

（2）兴趣小组准备从“不满意”的4位群众中随机选择2位进行回访，已知这4位群众中有2位来自甲片区，另2位来自乙片区，请用画树状图或列表的方法求出选择的群众来自甲片区的概率.

参考答案：

【答案】（1）50；18；（2）

【解析】

（1）根据“满意”的人数以及所占的百分比进行求解可得接受调查的人数，用所得的人数减去其余的即可得“非常满意”的人数；

（2）画树状图得到所有等可能的情况以及符合要求的情况数，利用概率公式进行计算即可得.

（1）∵满意的有20人，占40%，

∴此次调查中接受调查的人数：20÷40%=50（人）；

此次调查中结果为非常满意的人数为：50-4-8-20=18（人），

故答案为：50，18；

（2）画树状图得：

∵共有12种等可能的结果，选择的市民均来自甲区的有2种情况，

∴选择的市民均来自甲区的概率为：.

关闭