
【题目】如图,四边形ABCD是矩形,![]() ,
,![]() ,点P是对角线AC上的动点
,点P是对角线AC上的动点![]() 不与点A,C重合
不与点A,C重合![]() ,连接PD,作
,连接PD,作![]() 交射线BC于点E,以线段PD,PE为邻边作矩形PEFD.
交射线BC于点E,以线段PD,PE为邻边作矩形PEFD.

![]() 线段PD的最小值为______;
线段PD的最小值为______;
![]() 求证:
求证:![]() ,并求矩形PEFD面积的最小值;
,并求矩形PEFD面积的最小值;
![]() 是否存在这样的点P,使得
是否存在这样的点P,使得![]() 是等腰三角形?若存在,请求出PE的长;若不存在,请说明理由.
是等腰三角形?若存在,请求出PE的长;若不存在,请说明理由.
【答案】(1)![]() ;(2)证明见解析;(3) PE的长为
;(2)证明见解析;(3) PE的长为![]() 或
或![]() .
.
【解析】
![]() 如图1中,根据垂线段最短可知,当
如图1中,根据垂线段最短可知,当![]() 时,DP的值最小
时,DP的值最小![]() 利用面积法即可解决问题;
利用面积法即可解决问题;
![]() 如图2中,连接DE、PF交于点O,连接FC,
如图2中,连接DE、PF交于点O,连接FC,![]() 首先证明D、P、E、C、F五点共圆,由
首先证明D、P、E、C、F五点共圆,由![]() ∽
∽![]() ,推出
,推出![]() ,即可解决问题;
,即可解决问题;
![]() 分两种情形:点E在线段BC上,点E在线段BC的延长线上,分别求解即可解决问题;
分两种情形:点E在线段BC上,点E在线段BC的延长线上,分别求解即可解决问题;
![]() 解:如图1中,根据垂线段最短可知,当
解:如图1中,根据垂线段最短可知,当![]() 时,DP的值最小.
时,DP的值最小.
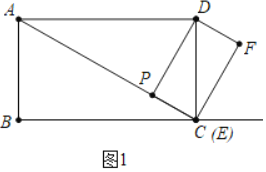
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
故答案为![]() .
.
![]() 证明:如图2中,连接DE、PF交于点O,连接FC,OC.
证明:如图2中,连接DE、PF交于点O,连接FC,OC.
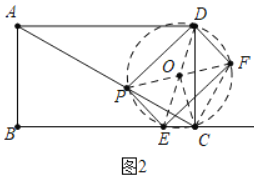
![]() 四边形DPEF是矩形,
四边形DPEF是矩形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 、P、E、C、F五点共圆,
、P、E、C、F五点共圆,
![]() 是直径,
是直径,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
∴S矩形PEFD=PE·PD=![]() PD2.
PD2.
∵PD的最小值是![]() ,
,
∴矩形PEFD面积的最小值是=![]() ×(
×(![]() )2=
)2=![]() .
.
![]() 解:如图3中,设AC交DE于H.
解:如图3中,设AC交DE于H.
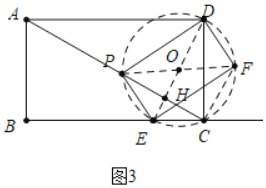
当![]() 时,易证
时,易证![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
如图4中,
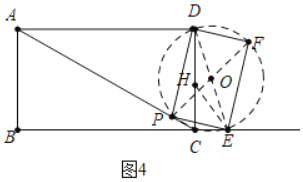
当![]() 时,
时,![]() ,
,
![]() ,
,
在CD上取一点H,速度![]() ,则
,则![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
综上所述,PE的长为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
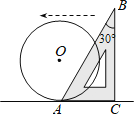
【题目】如图,半径为4的![]() 与含有
与含有![]() 角的真角三角板ABC的边AC切于点A,将直角三角板沿CA边所在的直线向左平移,当平移到AB与
角的真角三角板ABC的边AC切于点A,将直角三角板沿CA边所在的直线向左平移,当平移到AB与![]() 相切时,该直角三角板平移的距离为
相切时,该直角三角板平移的距离为![]()
![]()
A. 2 B. ![]() C. 4 D.
C. 4 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列条件,能判定△ABC≌△DEF的是( )
A.AB=DE,BC=EF,∠A=∠DB.∠A=∠D,∠C=∠F,AC=EF
C.∠B=∠E,∠A=∠D,AC=EFD.AB=DE,BC=EF,∠B=∠E
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠A=145°,∠D=75°.

(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)①如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
②在①的条件下,若延长BA、CD交于点F(如图4),将原来条件“∠A=145°,∠D=75°”改为“∠F=40°”,其他条件不变,∠BEC的度数会发生变化吗?若不变,请说明理由;若变化,求出∠BEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的一个动点(点
边上的一个动点(点![]() 不与点
不与点![]() ,点
,点![]() 重合),在
重合),在![]() 上取一点
上取一点![]() ,且∠CDE=50°.
,且∠CDE=50°.

(1)当![]() 时,求证:
时,求证:![]() ;
;
(2)当![]() 是等腰三角形时,
是等腰三角形时,![]() 的度数为
的度数为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知CE⊥AB于点E,BD⊥AC于点D,BD与CE交于点O,且AO平分∠BAC.
(1)图中有多少对全等三角形?请你一一列举出来(不要求说明理由).
(2)小明说:欲说明BE=CD,可先说明△AOE≌△AOD得到AE=AD,再说明△ADB≌△AEC得到AB=AC,然后利用等式的性质即可得到BE=CD,请问他的说法正确吗?如果不正确,请说明理由;如果正确,请按他的思路写出推导过程.
(3)要得到BE=CD,你还有其他的思路吗?请仿照小明的说法具体说一说你的想法.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com