【题目】如图所示，已知AD∥BC，AB⊥BC，CD⊥DE，CD=ED，AD=6，BC=9，则△ADE的面积为_____．
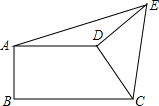
【答案】9．
【解析】
知道AD的长，只要求出AD边上的高，就可以求出△ADE的面积；过点D作DG⊥BC于G，过点E作EF⊥AD交AD的延长线于F，构造出△EDF≌△CDG，求出GC的长，即为EF的长，利用三角形的面积公式解答即可．
过点D作DG⊥BC于G，过点E作EF⊥AD交AD的延长线于F，如图所示：
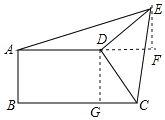
则四边形ABGD是矩形，
∴AD=BG，
∵∠EDF+∠FDC=90°，
∠GDC+∠FDC=90°，
∴∠EDF=∠GDC，
在△EDF和△CDG中，
，
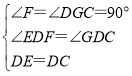∴△EDF≌△CDG（AAS），
∴EF=CG=BC-BG=BC-AD=9-6=3，
∴S△ADE=
ADEF=×6×3=9，
故答案为：9．
考前必练系列答案科目：初中数学 来源： 题型：
【题目】如图：有一块三角形状的土地平均分给四户人家，现有四种不同的分法，
如图中，D、E、F分别是BC、AC、AB的中点，G、H分别是BF、AF的中点
，其中正确的分法有
A. 1种 B. 2种 C. 3种 D. 4种
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，在△ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD=DC，则∠C的大小是（ ）
A.20°B.30°C.25°D.15°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将半径为2，圆心角为120°的扇形OAB绕点A逆时针旋转60°，点O，B的对应点分别为O′，B′，连接BB′，则图中阴影部分的面积是( )
A. 
B. 2
－
C. 2－ D. 4－
查看答案和解析>>
科目：初中数学 来源： 题型：
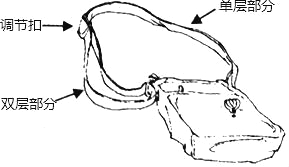
【题目】如图，是一种斜挎包，其挎带由双层部分、单层部分和调节扣构成．小敏用后发现，通过调节扣加长或缩短单层部分的长度，可以使挎带的长度（单层部分与双层部分长度的和，其中调节扣所占的长度忽略不计）加长或缩短．设单层部分的长度为xcm，双层部分的长度为ycm，经测量，得到如下数据：
单层部分的长度x（cm） | … | 4 | 6 | 8 | 10 | … | 150 |
双层部分的长度y（cm） | … | 73 | 72 | 71 | … |
（1）根据表中数据的规律，完成以下表格，并直接写出y关于x的函数解析式；
（2）根据小敏的身高和习惯，挎带的长度为120cm时，背起来正合适，请求出此时单层部分的长度；
（3）设挎带的长度为lcm，求l的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD是矩形，
，
，点P是对角线AC上的动点
不与点A，C重合
，连接PD，作
交射线BC于点E，以线段PD，PE为邻边作矩形PEFD．
线段PD的最小值为______；
求证：
，并求矩形PEFD面积的最小值；
是否存在这样的点P，使得
是等腰三角形？若存在，请求出PE的长；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC是边长为6 cm的等边三角形，动点P从A出发，以3 cm/s的速度，沿A-B-C向C运动，同时，动点Q从C出发沿CA方向以1 cm/s的速度向A运动，当其中一点运动到终点时，两点同时停止运动．设运动时间为t秒，当t= ____s，△APQ是直角三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克，大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元，小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后，该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克，进价不变，但在运输过程中小樱桃损耗了20%．若小樱桃的售价不变，要想让第二次赚的钱不少于第一次所赚钱的90%，大樱桃的售价最少应为多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
