
科目: 来源: 题型:
【题目】在四边形![]() 中,
中,![]() 是
是![]() 边上一点,
边上一点,![]() 点
点![]() 从
从![]() 出发以
出发以![]() 秒的速度沿线段
秒的速度沿线段![]() 运动,同时点
运动,同时点![]() 从
从![]() 出发,沿线段
出发,沿线段![]() 、射线
、射线![]() 运动,当
运动,当![]() 运动到
运动到![]() ,两点都停止运动.设运动时间为
,两点都停止运动.设运动时间为![]() (秒):
(秒):

(1)当![]() 与
与![]() 的速度相同,且
的速度相同,且![]() 时,求证:
时,求证:![]()
(2)当![]() 与
与![]() 的速度不同,且
的速度不同,且![]() 分别在
分别在![]() 上运动时(如图1),若
上运动时(如图1),若![]() 与
与![]() 全等,求此时
全等,求此时![]() 的速度和
的速度和![]() 值;
值;
(3)当![]() 运动到
运动到![]() 上,
上,![]() 运动到射线
运动到射线![]() 上(如图2),若
上(如图2),若![]() 的速度为
的速度为![]() 秒,是否存在恰当的边
秒,是否存在恰当的边![]() 的长,使在运动过程中某一时刻刚好
的长,使在运动过程中某一时刻刚好![]() 与
与![]() 全等,若存在,请求出此时
全等,若存在,请求出此时![]() 的值和边
的值和边![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
①请画出△ABC关于y轴对称的△A1B1C1;
②请画出△ABC关于x轴对称的△A2B2C2的各点坐标;
③在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出点P的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,到达目的地后停止,设慢车行驶时间为![]() 小时,两车之间的距离为
小时,两车之间的距离为![]() 千米,两者的关系如图所示,根据图象探究:
千米,两者的关系如图所示,根据图象探究:

(1)看图填空:两车出发 小时,两车相遇;
(2)求快车和慢车的速度;
(3)求线段![]() 所表示的
所表示的![]() 与
与![]() 的关系式,并求两车行驶
的关系式,并求两车行驶![]() 小时两车相距多少千米.
小时两车相距多少千米.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.
(1)求证:△ADE≌△BEC;
(2)若AD=6,AB=14,请求出CD的长.

查看答案和解析>>
科目: 来源: 题型:
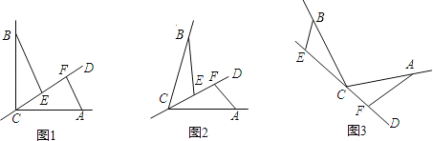
【题目】CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则BE_____CF;EF_____|BE﹣AF|(填“>”,“<”或“=”);
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件_____,使①中的两个结论仍然成立。
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想并给出理由。.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知一元二次方程2x2+2x﹣1=0的两个根为x1,x2,且x1<x2,下列结论正确的是( )
A. x1+x2=1 B. x1x2=﹣1 C. |x1|<|x2| D. x12+x1=![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,CD、CE分别是△ABC的高和角平分线.
(1)若∠A=30°,∠B=50°,求∠ECD的度数;
(2)试用含有∠A、∠B的代数式表示∠ECD(不必证明)

查看答案和解析>>
科目: 来源: 题型:
【题目】某水果店以每千克4元的价格购进一批水果,由于销售状况良好,该店又购进同一种水果,第二次进货价格比第一次每千克便宜了0.5元,所购水果重量恰好是第一次购进水果重量的2倍,这样该水果店两次购进水果共花去了2200元.
(1)该水果店两次分别购买了多少元的水果?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的水果有3%的损耗,第二次购进的水果有5%的损耗,该水果店希望售完这些水果获利不低于1244元,则该水果每千克售价至少为多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点C为线段AB上一点,△DAC、△ECB都是等边三角形,AE、DC交于点M,DB、EC交于点N,DB、AE交于点P,连接MN,下列说法中正确的个数有( )

①MN∥AB;②∠DPM=60°;③∠DAP=∠PEC;④△ACM≌△DCN;⑤若∠DBC=30°,则∠AEB=80°
A.2个B.3个C.4个D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com