【题目】阅读材料：大家知道是无理数是无限不循环小数，因此的小数部分我们不可能全部地写出来，于是小明用来表示的小数部分，你同意小明的表示方法吗？事实上，小明的表示方法是有道理的，因为的整数部分是1，将这个数减去其整数部分，差就是小数部分。又例如：因为,即，所以的整数部分为2，小数部分为,请解答下列问题：

(1) 如果的小数部分为a，的整数部分为b，求的值；

(2)已知，其中x是整数，且，求的值.

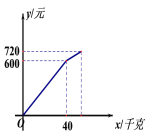
(1)降价前苹果的销售单价是 元/千克；

(2)求降价后销售金额y(元)与销售量x(千克)之间的函数表达式，并写出自变量的取值范围；

(3)该水果店这次销售苹果盈利了多少元？

（1）若OF+BE=AB，求证：CF=CE.

（2）如图2，∠ECF=45°， S△ECF=6，求S△BEF的值.

(1)求证:BE=CF

(2)如图2,过点D作DG⊥DF交AB于点G,连结GF,请你判断BG+CF与GF的大小关系，并说明理由.

(1)求证:Rt△ABE≌Rt△CBF

(2)若∠AEC=105°,求∠BCF的度数.

（1）以过点A的直线为折痕折叠纸片，使点B恰好落在AD边上，折痕与BC边交于点E（如图2）；

（2）以过点E的直线为折痕折叠纸片，使点A落在BC边上，折痕EF交AD边于点F（如图3）；

（3）将纸片收展平，那么∠AFE的度数为（　　）

A. 60° B. 67.5° C. 72° D. 75°

【题目】如图，在平面直角坐标系xOy中，一次函数y=kx+b的图象与反比例函数y=的图象相交于点A（m，3）、B（﹣6，n），与x轴交于点C．

（1）求一次函数y=kx+b的关系式；

（2）结合图象，直接写出满足kx+b＞的x的取值范围；

（3）若点P在x轴上，且S△ACP=S△BOC，求点P的坐标．

【题目】某班为了解学生一学期做义工的时间情况，对全班50名学生进行调查，按做义工的时间（单位：小时），将学生分成五类： 类（ ），类（），类（），类（），类（），绘制成尚不完整的条形统计图如图11.

根据以上信息，解答下列问题：

（1） 类学生有_________人，补全条形统计图；

（2）类学生人数占被调查总人数的__________%；

（3）从该班做义工时间在的学生中任选2人，求这2人做义工时间都在 中的概率．