
科目: 来源: 题型:
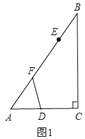
【题目】(本题6分)如图,已知△ABC,∠C=Rt∠,AC<BC,D为BC上一点,且到A,B两点的距离相等.

(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=37°,求∠CAD的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图①,已知:在△ABC中,∠BAC=90°,AB=AC,直线L经过点A,BD⊥直线L,CE⊥直线L,垂足分别为点D、E.证明:DE=BD+CE.
(2)组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线L上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图③,过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,AH是BC边上的高,延长HA交EG于点I,求证:I是EG的中点.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 由
由![]() 出发沿
出发沿![]() 向点
向点![]() 匀速运动,同时点
匀速运动,同时点![]() 由
由![]() 出发沿
出发沿![]() 向点
向点![]() 匀速运动,它们的速度相同,点
匀速运动,它们的速度相同,点![]() 在
在![]() 上,
上,![]() ,且点
,且点![]() 在点
在点![]() 的下方,当点
的下方,当点![]() 到达点
到达点![]() 时,点
时,点![]() ,
,![]() 也停止运动,连接
也停止运动,连接![]() ,设
,设![]() .解答下列问题:
.解答下列问题:
![]() 如图
如图![]() ,当
,当![]() 为何值时,
为何值时,![]() 为直角三角形;
为直角三角形;
![]() 如图
如图![]() ,把
,把![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 落在
落在![]() 点.
点.
①当![]() 为何值时,四边形
为何值时,四边形![]() 为菱形?并求出菱形的面积;
为菱形?并求出菱形的面积;
②如图![]() ,分别取
,分别取![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,在整个运动过程中,则线段
,在整个运动过程中,则线段![]() 扫过的区域的形状为________,其面积为________.
扫过的区域的形状为________,其面积为________.


查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=BC,AD⊥BC于点D,点E为AC中点且BE平分∠ABD,连接BE交AD于点F,且BF=AC,过点D作DG∥AB,交AC于点G.
求证:
(1)∠BAD=2∠DAC
(2)EF=EG.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,且AD=2,AC=BC=![]() .
.
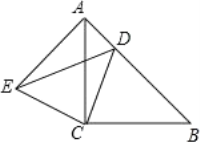
(1)证明:△ACE≌△BCD;
(2)求四边形ADCE的面积;
(3)求ED的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数y=x+m的图象交y轴于点D,且它与正比例函数![]() 的图象交于点A(2,n),设x轴上有一点P,过点P作x轴的垂线(垂线位于点A的右侧),分别交
的图象交于点A(2,n),设x轴上有一点P,过点P作x轴的垂线(垂线位于点A的右侧),分别交![]() 和y=x+m的图象与点B、C.
和y=x+m的图象与点B、C.
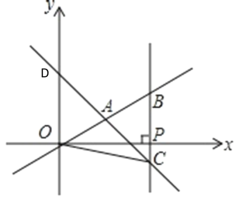
(1)求m和n的值;
(2)若BC=OD,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为![]() 个单位长度的正方形,
个单位长度的正方形,![]() 的顶点都在格点上,建立平面直角坐标系.
的顶点都在格点上,建立平面直角坐标系.

![]() 点
点![]() 的坐标为________,点
的坐标为________,点![]() 的坐标为________;
的坐标为________;
![]() 以原点
以原点![]() 为位似中心,将
为位似中心,将![]() 放大,使变换后得到的
放大,使变换后得到的![]() 与
与![]() 对应边的比为
对应边的比为![]() .请在网格内画出
.请在网格内画出![]() ,并写出点
,并写出点![]() 的坐标:________;
的坐标:________;
![]() 将
将![]() 向左平移
向左平移![]() 个单位,请画出平移后的
个单位,请画出平移后的![]() ;若
;若![]() 为
为![]() 内的一点,其坐标为
内的一点,其坐标为![]() ,则平移后点
,则平移后点![]() 的对应点
的对应点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】(题文)如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线![]() 相交于A(1,
相交于A(1,![]() ),B(4,0)两点.
),B(4,0)两点.

(1)求出抛物线的解析式;
(2)在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN,求出![]() 的值,并求出此时点M的坐标.
的值,并求出此时点M的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.

(1)求证:BE是⊙O的切线;
(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BGBA=48,FG=![]() ,DF=2BF,求AH的值.
,DF=2BF,求AH的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com