
科目: 来源: 题型:
【题目】将直角三角板ABC绕直角顶点C逆时针旋转角度![]() ,得到△DCE,其中CE与AB交于点F,∠ABC=30°,连接BE,若△BEF为等腰三角形(即有两内角相等),则旋转角
,得到△DCE,其中CE与AB交于点F,∠ABC=30°,连接BE,若△BEF为等腰三角形(即有两内角相等),则旋转角![]() 的值为________.
的值为________.

查看答案和解析>>
科目: 来源: 题型:
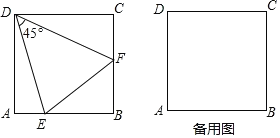
【题目】如图,在正方形ABCD中,E为直线AB上的动点(不与A,B重合),作射线DE并绕点D逆时针旋转45°,交直线BC边于点F,连结EF.
探究:当点E在边AB上,求证:EF=AE+CF.
应用:(1)当点E在边AB上,且AD=2时,则△BEF的周长是______.
(2)当点E不在边AB上时,EF,AE,CF三者的数量关系是______.
查看答案和解析>>
科目: 来源: 题型:
【题目】有一个安装有进出水管的30升容器,水管每单位时间内进出的水量是一定的,设从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到水量y(升)与时间x(分)之间的函数关系如图所示根据图象信息给出下列说法:
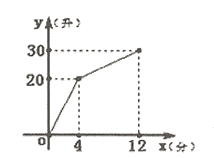
①每分钟进水5升;
②当![]() 时,容器中水量在减少;
时,容器中水量在减少;
③若12分钟后只放水,不进水,还要8分钟可以把水放完;
④若从一开始进出水管同时打开需要24分钟可以将容器灌满.
以下说法中正确的有( )
A.①B.①②C.①④D.①②④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,CA=CB,CD=CE,∠ACB=∠DCE=α.
(1)求证:BE=AD;

(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.

查看答案和解析>>
科目: 来源: 题型:
【题目】端午节期间,某食品店平均每天可卖出300只粽子,卖出1只粽子的利润是1元.经调查发现,零售单价每降0.1元,每天可多卖出100只粽子.为了使每天获取的利润更多,该店决定把零售单价下降m(0<m<1)元.
(1)零售单价下降m元后,该店平均每天可卖出_____只粽子,利润为_____元.
(2)在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润是420元并且卖出的粽子更多?
查看答案和解析>>
科目: 来源: 题型:
【题目】某文化用品商店用![]() 元采购一批书包,上市后发现供不应求,很快销售完了.商店又去采购第二批同样款式的书包,进货单价比第一次高
元采购一批书包,上市后发现供不应求,很快销售完了.商店又去采购第二批同样款式的书包,进货单价比第一次高![]() 元,商店用了
元,商店用了![]() 元,所购数量是第一次的
元,所购数量是第一次的![]() 倍.
倍.
(1)求第一批采购的书包的单价是多少元?
(2)若商店按售价为每个书包![]() 元,销售完这两批书包,总共获利多少元?
元,销售完这两批书包,总共获利多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】用适当的方法解方程:
(1)25 y 2- 16 = 0; (2)y 2+ 2 y-99=0;
(3)3x 2 + 2x -3=0; (4)(2x + 1)2 =3(2x + 1).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,完成下列推理过程:
如图所示,点E在![]() 外部,点D在BC边上,DE交AC于F,若
外部,点D在BC边上,DE交AC于F,若![]() ,
,![]() ,
,
求证:![]() .
.

证明:∵![]() (已知),
(已知),
![]() (________________),
(________________),
∴![]() (________________),
(________________),
又∵![]() ,
,
∴________![]() ________
________![]() (________),
(________),
即![]() ,
,
在![]() 和
和![]() 中
中
![]() (已证)
(已证)
∵![]() (已知)
(已知)
![]() (已证)
(已证)
∴![]() (________).
(________).
∴![]() (________________)
(________________)
查看答案和解析>>
科目: 来源: 题型:
【题目】数学活动–探究特殊的平行四边形.
问题情境
如图,在四边形![]() 中,
中,![]() 为对角线,
为对角线,![]() ,
,![]() .请你添加条件,使它们成为特殊的平行四边形.
.请你添加条件,使它们成为特殊的平行四边形.
提出问题

![]() 第一小组添加的条件是“
第一小组添加的条件是“![]() ”,则四边形
”,则四边形![]() 是菱形.请你证明;
是菱形.请你证明;
![]() 第二小组添加的条件是“
第二小组添加的条件是“![]() ,
,![]() ”,则四边形
”,则四边形![]() 是正方形.请你证明.
是正方形.请你证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com