（1）求两直线与y轴交点A，B的坐标；

（2）求两直线交点C的坐标；

（3）求△ABC的面积．

（1）判断线段DE、FG的位置关系，并说明理由；

（2）连结CG，求证：四边形CBEG是正方形．

【题目】在如图的直角坐标系中，画出函数的图象，并结合图象回答下列问题：

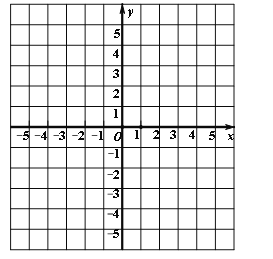
（1）y的值随x值的增大而______（填“增大”或“减小”）；

（2）图象与x轴的交点坐标是_____；图象与y轴的交点坐标是______；

（3）当x 时，y ＜0 ；

【题目】如图是二次函数图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）．下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（，y2）是抛物线上两点，则

y1＞y2．其中说法正确的是（ ）

A. ①② B. ②③ C. ①②④ D. ②③④

(1)如图①，在△ABC 中，∠B=30°，E 是 AB 边上的点，过点 E 作 EF⊥BC 于 F，则的值为 .

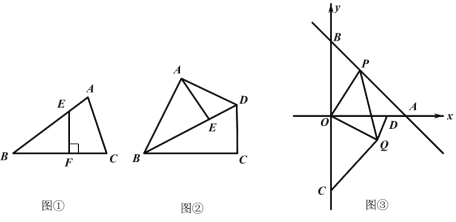
（2）如图②，在四边形 ABCD 中，AB=BC=6,∠ABC=60°，对角线 BD 平分∠ABC，点E 是对角线 BD 上一点，求 AE+ BE的最小值.

问题解决

（3）如图③，在平面直角坐标系中，直线 y -x 4 分别于 x 轴，y 轴交于点 A、B，点 P 为直线 AB 上的动点，以 OP 为边在其下方作等腰 Rt△OPQ 且∠POQ=90°.已知点C（0，-4），点 D（3,0）连接 CQ、DQ,那么DQ CQ是否存在最小值，若存在求出其最小值及此时点 P 的坐标，若不存在请说明理由.

A. B. 2 C. 3 D. 2

（1）求每个热水壶和保温杯的采购单价各是多少元?

（2）若商场计划再购进同种型号的热水壶和保温杯共 80 个，求所需购货资金 w（元） ，购买热水壶的数量 m(个)的函数表达式.

（3）在（2）的基础上，若准备购买保温杯的数量是热水壶数量的 3 倍，则该商店需要准备多少元的购货资金?