
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形![]() 的三个顶点
的三个顶点![]() 、
、![]() 、
、![]() .以
.以![]() 为顶点的抛物线
为顶点的抛物线![]() 过点
过点![]() .动点
.动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度沿线段
个单位的速度沿线段![]() 向点
向点![]() 运动,运动时间为
运动,运动时间为![]() 秒.过点
秒.过点![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() ,交
,交![]() 于点
于点![]() .
.
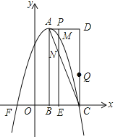
![]() 直接写出点
直接写出点![]() 的坐标,并求出抛物线的解析式;
的坐标,并求出抛物线的解析式;
![]() 当
当![]() 为何值时,
为何值时,![]() 的面积最大?最大值为多少?
的面积最大?最大值为多少?
查看答案和解析>>
科目: 来源: 题型:
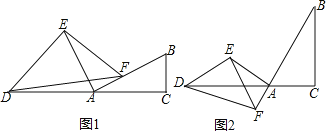
【题目】如图1所示,在Rt△ABC中,∠C=90°,点D是线段CA延长线上一点,且AD=AB,点F是线段AB上一点,连接DF,以DF为斜边作等腰Rt△DFE,连接EA,EA满足条件EA⊥AB,
(1)若∠AEF=20°,∠ADE=50°,BC=2,求AB的长度.
(2)求证:AE=AF+BC.
(3)如图2,点F是线段BA延长线上一点,探究AE、AF、BC之间的数量关系,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】某水果店销售某种水果,原来每箱售价![]() 元,每星期可卖
元,每星期可卖![]() 箱.为了促销,该水果店决定降价销售.市场调查反映:每降价
箱.为了促销,该水果店决定降价销售.市场调查反映:每降价![]() 元,每星期可多卖
元,每星期可多卖![]() 箱.已知该水果每箱的进价是
箱.已知该水果每箱的进价是![]() 元,设该水果每箱售价
元,设该水果每箱售价![]() 元,每星期的销售量为
元,每星期的销售量为![]() 箱.
箱.
![]() 求
求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 当每箱售价定为多少元时,每星期的销售利润最大,最大利润多少元?
当每箱售价定为多少元时,每星期的销售利润最大,最大利润多少元?
![]() 若该水果店销售这种水果每星期想要获得不低于
若该水果店销售这种水果每星期想要获得不低于![]() 元的利润,每星期至少要销售该水果多少箱?
元的利润,每星期至少要销售该水果多少箱?
查看答案和解析>>
科目: 来源: 题型:
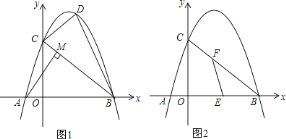
【题目】如图![]() ,在平面直角坐标系中,直线
,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,点
,点![]() 为
为![]() 轴负半轴上一点,
轴负半轴上一点,![]() 于点
于点![]() 交
交![]() 轴于点
轴于点![]() ,满足
,满足![]() .已知抛物线
.已知抛物线![]() 经过点
经过点![]() 、
、![]() 、
、![]() .
.
![]() 求抛物线的函数关系式;
求抛物线的函数关系式;
![]() 连接
连接![]() ,点
,点![]() 在线段
在线段![]() 上方的抛物线上,连接
上方的抛物线上,连接![]() 、
、![]() ,若
,若![]() 和
和![]() 面积满足
面积满足![]() ,求点
,求点![]() 的坐标;
的坐标;
![]() 如图
如图![]() ,
,![]() 为
为![]() 中点,设
中点,设![]() 为线段
为线段![]() 上一点(不含端点),连接
上一点(不含端点),连接![]() .一动点
.一动点![]() 从
从![]() 出发,沿线段
出发,沿线段![]() 以每秒
以每秒![]() 个单位的速度运动到
个单位的速度运动到![]() ,再沿着线段
,再沿着线段![]() 以每秒
以每秒![]() 个单位的速度运动到
个单位的速度运动到![]() 后停止.若点
后停止.若点![]() 在整个运动过程中用时最少,请直接写出最少时间和此时点
在整个运动过程中用时最少,请直接写出最少时间和此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
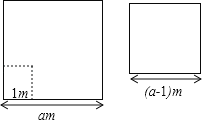
【题目】如图,“主收1号”小麦的试验田是边长为am(a>1)的正方形去掉一个边长为1m的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(a﹣1)m的正方形,两块试验田的小麦都收获了500kg.
(1)哪种小麦的单位面积产量高?
(2)若高的单位面积产量是低的单位面积产量的![]() (kg)倍,求a的值
(kg)倍,求a的值
(3)利用(2)中所求的a的值,分解因式x2﹣ax﹣108=_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】近年来,安全快捷、平稳舒适的中国高铁,为世界高速铁路的发展树立了新的标杆,随着中国特色社会主义进入新时代,作为“中国名片”的高速铁路也将踏上自己的新征程,这就意味着今后外出旅行的路程与时间将大大缩短,但也有不少游客根据自已的喜好依然选择乘坐普通列车,已知从咸宁地到某地的普通列车行驶路程是520千米,是高铁行驶路程的1.3倍,请完成以下问题:
(1)高铁行驶的路程为_____千米.
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
查看答案和解析>>
科目: 来源: 题型:
【题目】解决下列两个问题:
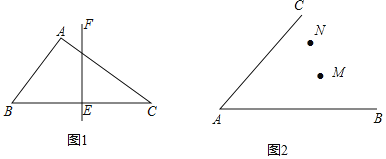
(1)如图1,在△ABC中,AB=4,AC=6,BC=7,EF垂直平分BC,P为直线EF上一动点,PA+PB的最小值为______,并在图中标出当PA+PB取最小值时点P的位置.
(2)如图2,点M、N在∠BAC的内部,请在∠BAC的内部求作一点P,使得点P到∠BAC两边的距离相等,且使PM=PN.(尺规作图,保留作图痕迹,无需证明)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
恒成立的结论有 .(把你认为正确的序号都填上)

查看答案和解析>>
科目: 来源: 题型:
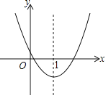
【题目】如图,二次函数![]() 的图象如图所示,则下列说法①
的图象如图所示,则下列说法①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() ;④当
;④当![]() 时,
时,![]() ;⑤关于
;⑤关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根.你认为其中正确的有( )
有两个不相等的实数根.你认为其中正确的有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD中,AB=2,AD=4,动点E在边BC上,与点B、C不重合,过点A作DE的垂线,交直线CD于点F.设DF=x,EC=y.
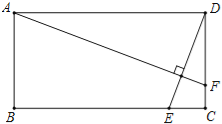
(1)求y关于x的函数关系式,并写出x的取值范围.
(2)当CF=1时,求EC的长.
(3)若直线AF与线段BC延长线交于点G,当△DBE与△DFG相似时,求DF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com