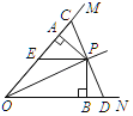
A.CP＝PDB.PA＝PBC.PE＝OED.OB＝CD

（1）求点B的坐标；

（2）如图2，连接DE，求证：BD﹣AE＝DE；

（3）如图3，若点F为（4，0），点P在第一象限内，连接PF，过P作PM⊥PF交y轴于点M，在PM上截取PN＝PF，连接PO、BN，过P作∠OPG＝45°交BN于点G，求证：点G是BN的中点．

已知a，b为非负实数，∵a+b﹣2=（）2+（）2﹣2=（﹣）2≥0，∴a+b≥2，当且仅当“a=b”时，等号成立．示例：当x＞0时，求y=x++1的最小值；

解：y=（x+）+1＞2=3，当x=，即x=1时，y的最小值为3．

（1）探究：当x＞0时，求y=的最小值；

（2）问题解决：随着人们生活水平的提高，汽车已成为越来越多家庭的交通工具，假设某种汽车的购车费用为10万元，每年应缴保险费等各类费用共计0.4万元，n年的保养，维修费用总和为万元，问这种汽车使用多少年报废最合算（即使用多少年的年平均费用最少，年平均费用=所有费用：年数n）？最少年平均费用为多少万元？

（1）求证：四边形AEBD是矩形；

（2）当△ABC满足什么条件时，矩形AEBD是正方形，并说明理由．

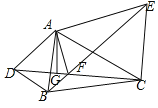
数学课上，老师出示了这样一道题：如图，△ABD和△ACE中，AB＝AD，AC＝AE，∠DAB＝∠CAE＝α，连接DC、BE交于点F，过A作AG⊥DC于点G，探究线段FG、FE、FC之间的数量关系，并证明．

同学们经过思考后，交流了自已的想法：

小明：“通过观察和度量，发现线段BE与线段DC相等．”

小伟：“通过观察发现，∠AFE与α存在某种数量关系．”

老师：“通过构造全等三角形，从而可以探究出线段FG、FE、FC之间的数量关系．”

（1）求证：BE＝CD；

（2）求∠AFE的度数（用含α的式子表示）；

（3）探究线段FG、FE、FC之间的数量关系，并证明．

（1）证明：四边形ACDE是平行四边形；

（2）若AC＝4，BD＝3，求△ADE的周长

(1)当D在线段BC上时,求证:△BAD≌△CAE；

(2)当点D运动到何处时，AC⊥DE，并说明理由；

(3)当CE∥AB时，若△ABD中最小角为20°，试探究∠ADB的度数(直接写出结果，无需写出求解过程).

(1)请你通过列表(或树状图)分别计算乘积是2的倍数和3的倍数的概率;

(2)你认为这个游戏公平吗?为什么?若你认为不公平,请你修改得分规则,使游戏对双方公平.

【题目】如图，已知正方形ABCD的边长为4，以AB为一边作等边△ABE，使点E落在正方形ABCD的内部，连接AC交BE于点F，连接CE、DE，则下列说法中：①△ADE≌△BCE；②∠ACE=30°；③AF=CF；④ =2+，其中正确的有（　　）

A. 1个 B. 2个 C. 3个 D. 4个