
科目: 来源: 题型:
【题目】如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,若AE=2,当EF+CF取得最小值时,则∠BCF的度数为_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)求点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】某商店将每件进价为80元的某种商店按每件110元出售,每天可售出100件.该商店想通过降低售价、增加销售量的方法来提高利润.经市场调查,发现这种商品每件每降价5元,每天的销售量可增加50件.设商品降价x元,每天销售该商品获得的利润为y元.
(1)求y(元)关于x(元)的函数关系式,并写出x的取值范围.
(2)求当x取何值时y最大?并求出y的最大值.
(3)若要是每天销售利润为3750元,且尽可能最大的向顾客让利,应将该商品降价多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.

(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目: 来源: 题型:
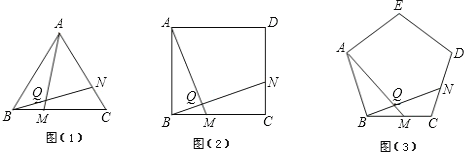
【题目】(1)如图(1),已知△ABC为正三角形,点M是BC上一点,点N是AC上一点,AM、BN相交于点Q,BM=CN.求出∠BQM的度数;
(2)将(1)中的“正△ABC”分别改为正方形ABCD、正五边形ABCDE、…正n边形ABCD…,“点N是AC上一点”改为点N是CD上一点,其余条件不变,分别推断出∠BQM等于多少度,将结论填入下表:
正多边形 | 正方形 | 正五边形 | …… | 正n边形 |
∠BQM的度数 |
|
| …… |
|
查看答案和解析>>
科目: 来源: 题型:
【题目】下列各组条件中,能够判定△ABC≌△DEF 的是( )
A. ∠A=∠D,∠B=∠E,∠C=∠FB. AB=DE,BC=EF,∠A=∠D
C. ∠B=∠E=90°,BC=EF,AC=DFD. ∠A=∠D,AB=DF,∠B=∠E
查看答案和解析>>
科目: 来源: 题型:
【题目】八年级的小明同学通到这样一道数学题目:△ABC为边长为4的等边三角形,E是边AB边上任意一动点,点D在CB的延长线上,且满足AE=BD.

(1)如图①,当点E为AB的中点时,DE= ;
(2)如图②,点E在运动过程中,DE与EC满足什么数量关系?请说明理由;
(3)如图③,F是AC的中点,连接EF.在AB边上是否存在点E,使得DE+EF值最小?若存在,求出这个最小值;若不存在,请说明理由.(直角三角形中,30°所对的边是斜边的一半)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知直线y=﹣![]() x+3与x轴、y轴分别交于A、C,以OA、OC为边在第一象限内作长方形OABC.
x+3与x轴、y轴分别交于A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)将△ABC沿B′D对折,使得点A与点C重合,折痕交AB于点D,求直线CD的解析式;
(2)若在x轴上存在点P,使△ADP为等腰三角形,求出符合条件的点P坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com