
科目: 来源: 题型:
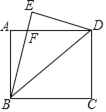
【题目】如图,将矩形ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
(1)求证:△ABF≌△EDF;
(2)若AB=6,BC=8,求AF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).

请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在2018年韶关市开展的“善美韶关情暖三江”的志愿者系列括动中,某志愿者组织筹集了部分资金,计划购买甲、乙两种书包若干个送给贫困山区的学生,已知每个甲种书包的价格比每个乙种书包的价格贵10元,用350元购买甲种书包的个数恰好与用300元购买乙种书包的个数相同,求甲、乙两种书包每个的价格各是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 经过点E(1,0)和F(5,0),并交y轴于D(0,-5);抛物线
经过点E(1,0)和F(5,0),并交y轴于D(0,-5);抛物线![]() :
:![]() (a≠0),
(a≠0),
(1)试求抛物线![]() 的函数解析式;
的函数解析式;
(2)求证: 抛物线 ![]() 与x轴一定有两个不同的交点;
与x轴一定有两个不同的交点;
(3)若a=1
①抛物线![]() 、
、![]() 顶点分别为 ( , )、( , ) ;当x的取值范围是_________ 时,抛物线
顶点分别为 ( , )、( , ) ;当x的取值范围是_________ 时,抛物线![]() 、
、![]() 上的点的纵坐标同时随横坐标增大而增大;
上的点的纵坐标同时随横坐标增大而增大;
②已知直线MN分别与x轴、![]() 、
、![]() 分别交于点P(m,0)、M、N,且MN∥y轴,当1≤m≤5时,求线段MN的最大值。
分别交于点P(m,0)、M、N,且MN∥y轴,当1≤m≤5时,求线段MN的最大值。
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)观察猜想
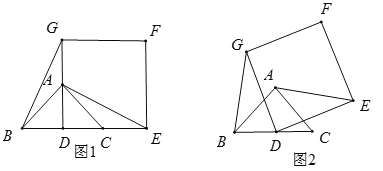
如图(1),在△ABC中,∠BAC=90°,AB=AC,点D是BC的中点.以点D为顶点作正方形DEFG,使点A,C分别在DG和DE上,连接AE,BG,则线段BG和AE的数量关系是_____;
(2)拓展探究
将正方形DEFG绕点D逆时针方向旋转一定角度后(旋转角度大于0°,小于或等于360°),如图2,则(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由.
(3)解决问题
若BC=DE=2,在(2)的旋转过程中,当AE为最大值时,直接写出AF的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知某种产品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查发现,该产品每降价1元,每星期可多卖出20件,由于供货方的原因销量不得超过380件,设这种产品每件降价x元(x为整数),每星期的销售利润为w元.
(1)求w与x之间的函数关系式,并写出自变量x的取值范围;
(2)该产品销售价定为每件多少元时,每星期的销售利润最大?最大利润是多少元?
(3)该产品销售价在什么范围时,每星期的销售利润不低于6000元,请直接写出结果.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点A在∠MON的边ON上,AB⊥OM于B,AE=OB,DE⊥ON于E,AD=AO,DC⊥OM于C.
(1)求证:四边形ABCD是矩形;
(2)若DE=3,OE=9,求AB、AD的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】某中学举办“校园好声音”朗诵大赛,根据初赛成绩,七年级和八年级各选出5名选手组成七年级代表队和八年级代表队参加学校决赛两个队各选出的5名选手的决赛成绩如图所示:
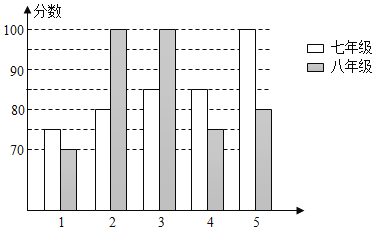
(1)根据所给信息填写表格;
平均数(分) | 中位数(分) | 众数(分) | |
七年级 | 85 | ||
八年级 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)若七年级代表队决赛成绩的方差为70,计算八年级代表队决赛成绩的方差,并判断哪个代表队的选手成绩较为稳定.
查看答案和解析>>
科目: 来源: 题型:
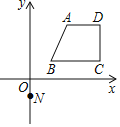
【题目】如图,过点N(0,-1)的直线y=kx+b与图中的四边形ABCD有不少于两个交点,其中A(2,3)、B(1,1)、C(4,1)、D(4,3),则k的取值范围____________
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A、B两点,与
与x轴交于A、B两点,与![]() 轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3.
轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3.

(1)求抛物线所对应的函数解析式.
(2)若点P为抛物线对称轴上的一个动点,求![]() PAC周长的最小值.
PAC周长的最小值.
(3)将AOC绕点C逆时针旋转90°,点A对应点为点G,问点G是否在该抛物线上?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com