
科目: 来源: 题型:
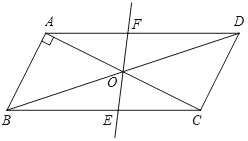
【题目】如图,在ABCD中,AB=1,BC=![]() ,对角线AC,BD交于O点,将直线AC绕点O顺时针旋转,分别交于BC,AD于点E,F.
,对角线AC,BD交于O点,将直线AC绕点O顺时针旋转,分别交于BC,AD于点E,F.
(1)证明:当旋转角为 时,四边形ABEF是平行四边形;
(2)在旋转过程中,四边形BEDF可能是菱形吗?如果不可能,请说明理由;如果可能,说明理由并求出此时AC绕点O顺时针旋转的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.
设每个房间每天的定价增加x元.求:
(1)房间每天的入住量y(间)关于x(元)的函数关系式;
(2)该宾馆每天的房间收费z(元)关于x(元)的函数关系式;
(3)该宾馆客房部每天的利润w(元)关于x(元)的函数关系式;当每个房间的定价为每天多少元时,w有最大值?最大值是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是__________

查看答案和解析>>
科目: 来源: 题型:
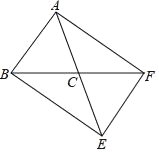
【题目】如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△EFC,连接AF、BE.
(1)求证:四边形ABEF是平行四边形;
(2)当∠ABC为多少度时,四边形ABEF为矩形?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
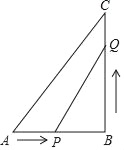
【题目】已知:如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于6cm2?
(2)在(1)中,△PQB的面积能否等于8cm2?说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列条件中,不能判断△ABC是直角三角形的是( )
A. a:b:c=3:4:5 B. ∠A:∠B:∠C=3:4:5
C. ∠A+∠B=∠C D. a:b:c=1:2:![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】两块等腰直角三角尺![]() 与
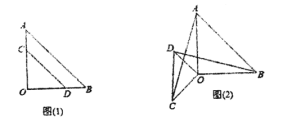
与![]() (不全等)如图(1)放置,则有结论:①
(不全等)如图(1)放置,则有结论:①![]() ②
②![]() ;若把三角尺
;若把三角尺![]() 绕着点
绕着点![]() 逆时针旋转一定的角度后,如图(2)所示,判断结论:①
逆时针旋转一定的角度后,如图(2)所示,判断结论:①![]() ②
②![]() 是否都还成立?若成立请给出证明,若不成立请说明理由.
是否都还成立?若成立请给出证明,若不成立请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,已知点P0的坐标为(2,0),将点P0绕着原点O按逆时针方向旋转60°得点P1,延长OP1到点P2,使OP2=2OP1,再将点P2绕着原点O按逆时针方向旋转60°得点P3,则点P3的坐标是_____.
查看答案和解析>>
科目: 来源: 题型:
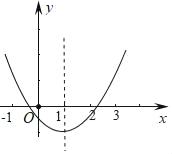
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则在下列各式子:①abc>0;②a+b+c>0;③a+c>b;④2a+b=0;⑤![]() =b2-4ac<0中,成立的式子有( )
=b2-4ac<0中,成立的式子有( )
A. ②④⑤ B. ②③⑤
C. ①②④ D. ①③④
查看答案和解析>>
科目: 来源: 题型:
【题目】(2017浙江省湖州市,第23题,10分)湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了20000kg淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养10天的总成本为30.4万元;放养20天的总成本为30.8万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是a万元,收购成本为b万元,求a和b的值;
(2)设这批淡水鱼放养t天后的质量为m(kg),销售单价为y元/kg.根据以往经验可知:m与t的函数关系为![]() ;y与t的函数关系如图所示.
;y与t的函数关系如图所示.
①分别求出当0≤t≤50和50<t≤100时,y与t的函数关系式;
②设将这批淡水鱼放养t天后一次性出售所得利润为W元,求当t为何值时,W最大?并求出最大值.(利润=销售总额﹣总成本)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com