
科目: 来源: 题型:
【题目】问题探究
(1)如图1,已知锐角△ABC中,点D在BC边上,当线段AD最短时,请你在图中画出点D的位置.
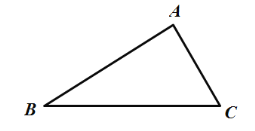
图1
(2)若一个四边形的四个顶点分别在一个三角形的三条边上;则称这个四边形为该三角形的内接四边形.
如图2,在Rt△ABC中,AB=6,BC=8,∠B=90°.矩形BEFG是△ABC的内接矩形,若EF=2,则矩形BEFG的面积为_________
如图3,在△ABC中,AB=![]() ,BC=8,∠B=45°,矩形DEFG是△ABC的一个内接矩形且D、E在边BC上.若EF=2,求矩形DEFG的面积;
,BC=8,∠B=45°,矩形DEFG是△ABC的一个内接矩形且D、E在边BC上.若EF=2,求矩形DEFG的面积;
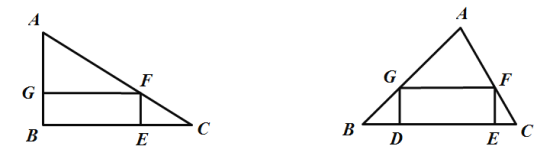
图2 图3
问题解决:
(3)如图4,△ABC是一块三角形木板余料,AB=6,BC=8,∠B=30°,木匠师傅想利用它裁下一块矩形DEFG木块,矩形DEFG是△ABC的一个内接矩形且D、E在边BC上,请在图4中画出对角线DF最短的矩形DEFG,请说明理由,并求出此时DF的长度.
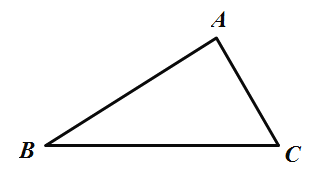
图4
查看答案和解析>>
科目: 来源: 题型:
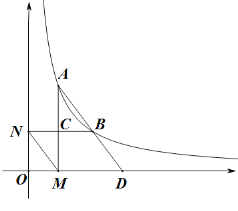
【题目】如图,已知反比例函数y=![]() (x>0,k是常数)的图象经过点A(1,4),点B(m,n),其中m>1,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.
(x>0,k是常数)的图象经过点A(1,4),点B(m,n),其中m>1,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.
(1)求出反比例函数解析式;
(2)求证:△ACB∽△NOM.
(3)延长线段AB,交x轴于点D,若点B恰好为AD的中点,求此时点B的坐标.
查看答案和解析>>
科目: 来源: 题型:
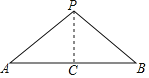
【题目】已知,如图,点![]() 在线段
在线段![]() 外,且
外,且![]() ,求证:点
,求证:点![]() 在线段
在线段![]() 的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )
的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )
A.作![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() B.过点
B.过点![]() 作
作![]() 于点
于点![]() 且
且![]()
C.取![]() 中点
中点![]() ,连接
,连接![]() D.过点
D.过点![]() 作
作![]() ,垂足为
,垂足为![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为

A.![]() B.3 C.1 D.
B.3 C.1 D.![]()
查看答案和解析>>
科目: 来源: 题型:
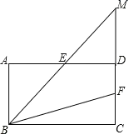
【题目】如图,在四边形ABCD中,AB∥CD,AB=CD,∠A=∠ADC,E,F分别为AD,CD的中点,连接BE,BF,延长BE交CD的延长线于点M.
(1)求证:四边形ABCD为矩形;
(2)若MD=6,BC=12,求BF的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两人在玩转盘游戏时,把两个可以自由转动的转盘A、B分成4等份、3等份的扇形区域,并在每一小区域内标上数字(如图所示),指针的位置固定.游戏规则:同时转动两个转盘,当转盘停止后,若指针所指两个区域的数字之和为3的倍数,甲胜;若指针所指两个区域的数字之和为4的倍数时,乙胜.如果指针落在分割线上,则需要重新转动转盘.

(1)试用列表或画树形图的方法,求甲获胜的概率;
(2)请问这个游戏规则对甲、乙双方公平吗?试说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料,并解答问题.
材料:将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
解:由分母为﹣x2+1,可设﹣x4﹣x2+3=(﹣x2+1)(x2+a)+b则﹣x4﹣x2+3=(﹣x2+1)(x2+a)+b=﹣x4﹣ax2+x2+a+b=﹣x4﹣(a﹣1)x2+(a+b)
∵对应任意x,上述等式均成立,∴![]() ,∴a=2,b=1
,∴a=2,b=1
∴![]() =
=![]() =
=![]() +
+![]() =x2+2+
=x2+2+![]() 这样,分式
这样,分式![]() 被拆分成了一个整式x2+2与一个分式
被拆分成了一个整式x2+2与一个分式![]() 的和.
的和.
解答:
(1)将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
(2)试说明![]() 的最小值为8.
的最小值为8.
查看答案和解析>>
科目: 来源: 题型:
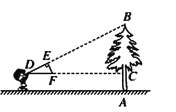
【题目】如图,小明同学用自制的直角三角形纸板DEF测量树AB的高度,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,求树AB的高度.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知△ABC是等边三角形, D、 E分别在边AB、AC上,且AD=CE,CD与BE相交于点O.
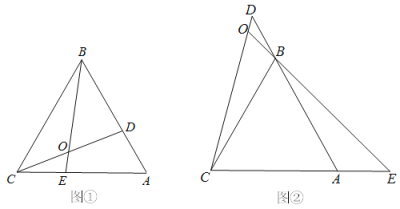
(1)如图①,求∠BOD的度数;
(2)如图②,如果点D、 E分别在边AB、CA的延长线上时,且AD=CE,求∠BOD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com