
科目: 来源: 题型:
【题目】如图,点P是∠BAC的平分线AD上一点,且∠BAC=30°,PE∥AB交AC于点E,已知AE=2,则点P到AB的距离是( )
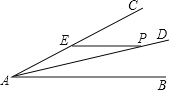
A.1.5B.![]() C.1D.2
C.1D.2
查看答案和解析>>
科目: 来源: 题型:
【题目】已知在平面直角坐标系![]() 中的点P和图形G,给出如下的定义:若在图形G上存在一点Q ,使得P、Q之间的距离等于1,则称P为图形G的关联点.
中的点P和图形G,给出如下的定义:若在图形G上存在一点Q ,使得P、Q之间的距离等于1,则称P为图形G的关联点.
(1)当⊙O的半径为1时:
①点![]() ,
, ![]() ,
, ![]() 中,⊙O的关联点有_____________________.
中,⊙O的关联点有_____________________.
②直线经过(0,1)点,且与![]() 轴垂直,点P在直线上.若P是⊙O的关联点,求点P的横坐标
轴垂直,点P在直线上.若P是⊙O的关联点,求点P的横坐标![]() 的取值范围.
的取值范围.
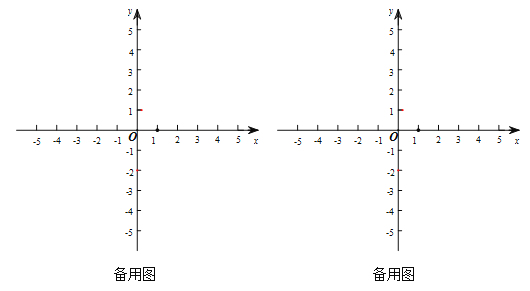
(2)已知正方形ABCD的边长为4,中心为原点,正方形各边都与坐标轴垂直.若正方形各边上的点都是某个圆的关联点,求圆的半径![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
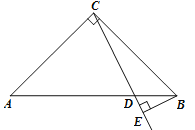
【题目】如图,已知Rt△ABC中,∠ACB=90°,AC=BC,D是线段AB上的一点(不与A、B重合).过点B作BE⊥CD,垂足为E.将线段CE绕点C顺时针旋转![]() ,得到线段CF,连结EF.设∠BCE度数为
,得到线段CF,连结EF.设∠BCE度数为![]() .
.
(1)①补全图形;
②试用含![]() 的代数式表示∠CDA.
的代数式表示∠CDA.
(2)若![]() ,求
,求![]() 的大小.
的大小.
(3)直接写出线段AB、BE、CF之间的数量关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线: ![]() .
.
(1)求抛物线的顶点坐标.
(2)若直线![]() 经过(2,0)点且与
经过(2,0)点且与![]() 轴垂直,直线
轴垂直,直线![]() 经过抛物线的顶点与坐标原点,且
经过抛物线的顶点与坐标原点,且![]() 与
与![]() 的交点P在抛物线上.求抛物线的表达式.
的交点P在抛物线上.求抛物线的表达式.
(3)已知点A(0,2),点A关于![]() 轴的对称点为点B.抛物线与线段AB恰有一个公共点,结合函数图象写出
轴的对称点为点B.抛物线与线段AB恰有一个公共点,结合函数图象写出![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】在下列命题中:①有一个外角是![]() 的等腰三角形是等边三角形;②有两个外角相等的等腰三角形是等边三角形;③有一边上的高也是这边上的中线的三角形是等边三角形;④三个外角都相等的三角形是等边三角形.正确的命题有( )
的等腰三角形是等边三角形;②有两个外角相等的等腰三角形是等边三角形;③有一边上的高也是这边上的中线的三角形是等边三角形;④三个外角都相等的三角形是等边三角形.正确的命题有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目: 来源: 题型:
【题目】做服装生意的王老板经营甲、乙两个店铺,每个店铺在同一段时间内都能售出A,B两种款式的服装合计30件,并且每售出一件A款式和B款式服装,甲店铺获毛利润分别为30元和40元,乙店铺获毛利润分别为27元和36元.某日王老板进货A款式服装35件,B款式服装25件.怎样分配给每个店铺各30件服装,使得在保证乙店铺毛利润不小于950元的前提下,王老板获取的总毛利润最大?最大的总毛利润是多少?
查看答案和解析>>
科目: 来源: 题型:
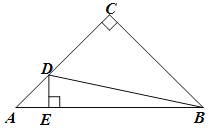
【题目】如图,Rt△ABC中, ![]() ,AC=BC,AB=4cm.动点D沿着A→C→B的方向从A点运动到B点.DE⊥AB,垂足为E.设AE长为
,AC=BC,AB=4cm.动点D沿着A→C→B的方向从A点运动到B点.DE⊥AB,垂足为E.设AE长为![]() cm,BD长为
cm,BD长为![]() cm(当D与A重合时,
cm(当D与A重合时, ![]() =4;当D与B重合时
=4;当D与B重合时![]() =0).
=0).
小云根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小云的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
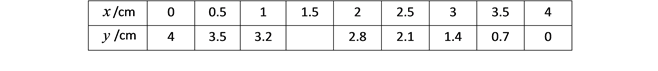
补全上面表格,要求结果保留一位小数.则![]() __________.
__________.
(2)在下面的网格中建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:当DB=AE时,AE的长度约为 cm.
查看答案和解析>>
科目: 来源: 题型:
【题目】“立定跳远”是我市初中毕业生体育测试项目之一.测试时,记录下学生立定跳远的成绩,然后按照评分标准转化为相应的分数,满分10分.其中男生立定跳远的评分标准如下:注:成绩栏里的每个范围,含最低值,不含最高值.
成绩(米) | … | 1.80~1.86 | 1.86~1.94 | 1.94~2.02 | 2.02~2.18 | 2.18~2.34 | 2.34~ |
得分(分) | … | 5 | 6 | 7 | 8 | 9 | 10 |
某校九年级有480名男生参加立定跳远测试,现从中随机抽取10名男生测试成绩(单位:分)如下:
1.96 2.38 2.56 2.04 2.34 2.17 2.60 2.26 1.87 2.32
请完成下列问题:
(1)求这10名男生立定跳远成绩的极差和平均数;
(2)求这10名男生立定跳远得分的中位数和众数;
(3)如果将9分(含9分)以上定为“优秀”,请你估计这480名男生中得优秀的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com