
科目: 来源: 题型:
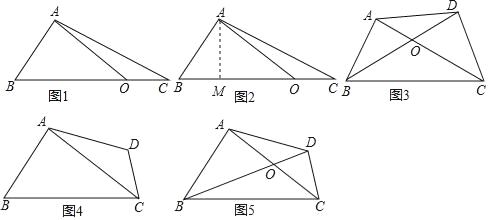
【题目】问题提出:某物业公司接收管理某小区后,准备进行绿化建设,现要将一块四边形的空地(如图5,四边形ABCD)铺上草皮,但由于年代久远,小区规划书上该空地的面积数据看不清了,仅仅留下两条对角线AC,BD的长度分别为20cm,30cm及夹角∠AOB为60°,你能利用这些数据,帮助物业人员求出这块空地的面积吗?
问题显然,要求四边形ABCD的面积,只要求出△ABD与△BCD(也可以是△ABC与△ACD)的面积,再相加就可以了.
建立模型:我们先来解决较简单的三角形的情况:
如图1,△ABC中,O为BC上任意一点(不与B,C两点重合),连接OA,OA=a,BC=b,∠AOB=α(α为OA与BC所夹较小的角),试用a,b,α表示△ABC的面积.
解:如图2,作AM⊥BC于点M,
∴△AOM为直角三角形.
又∵∠AOB=α,∴sinα=![]() 即AM=OAsinα
即AM=OAsinα
∴△ABC的面积=![]() BCAM=
BCAM=![]() BCOAsinα=
BCOAsinα=![]() absinα.
absinα.
问题解决:请你利用上面的方法,解决物业公司的问题.
如图3,四边形ABCD中,O为对角线AC,BD的交点,已知AC=20m,BD=30m,∠AOB=60°,求四边形ABCD的面积.(写出辅助线作法和必要的解答过程)
新建模型:若四边形ABCD中,O为对角线AC,BD的交点,已知AC=a,BD=b,∠AOB=α(α为OA与BC所夹较小的角),直接写出四边形ABCD的面积= .
模型应用:如图4,四边形ABCD中,AB+CD=BC,∠ABC=∠BCD=60°,已知AC=a,则四边形ABCD的面积为多少?(“新建模型”中的结论可直接利用)
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司营销A,B两种产品,根据市场调研,发现如下信息:
信息1:销售A种产品所获利润y(万元)与所售产品x(吨)之间存在二次函数关系![]() 。
。
当x=1时,y=1.4;当x=3时,y=3.6。
信息2:销售B种产品所获利润y(万元)与所售产品x(吨)之间存在正比例函数关系![]() 。
。
根据以上信息,解答下列问题:
(1)求二次函数解析式;
(2)该公司准备购进A,B两种产品共10吨,请设计一个营销方案,使销售A,B两种产品获得的利润之和最大,最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
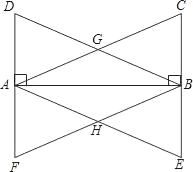
【题目】在Rt△ABC与Rt△ABD中,∠ABC=∠BAD=90°,AC=BD,AC,BD相交于点G,过点A作AE∥DB交CB的延长线于点E,过点B作BF∥CA交DA的延长线于点F,AE,BF相交于点H.
(1)证明:△ABD≌△BAC.
(2)四边形AHBG是什么样的四边形,请猜想并证明.
(3)若使四边形AHBG是正方形,还需在Rt△ABC添加一个什么条件?请添加条件并证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】有公路l1同侧、l2异侧的两个城镇A,B,如下图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不要求写出画法)
查看答案和解析>>
科目: 来源: 题型:
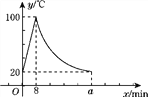
【题目】教师办公室有一种可以自动加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10 ℃,待加热到100 ℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例函数关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温均为20 ℃,接通电源后,水温y(℃)和通电时间x(min)之间的关系如图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的函数关系式;
(2)求出图中a的值;
(3)李老师这天早上7:30将饮水机电源打开,若他想在8:10上课前喝到不低于40 ℃的开水,则他需要在什么时间段内接水?
查看答案和解析>>
科目: 来源: 题型:
【题目】南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向![]() 海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.

查看答案和解析>>
科目: 来源: 题型:
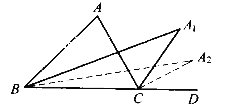
【题目】如图,在![]() ABC中,
ABC中, ![]() A=80
A=80![]() ,
, ![]() ABC与
ABC与![]() ACD的平分线交于点A1,得
ACD的平分线交于点A1,得![]() A1;
A1; ![]() A1BC与
A1BC与![]() A1CD的平分线相交于点A2,得
A1CD的平分线相交于点A2,得![]() A2;……;
A2;……; ![]() A7BC与
A7BC与![]() A7CD的平分线相交于点A8,得
A7CD的平分线相交于点A8,得![]() A8,则
A8,则![]() A8的度数为()
A8的度数为()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到奶汁的概率是 ;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶汁的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,∠ABC,∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的是:①△BDF,△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长为AB+AC;④BD=CE.( )
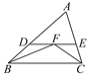
A. ③④ B. ①② C. ①②③ D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com