
科目: 来源: 题型:
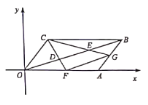
【题目】在平面直角坐标系中,平行四边形![]() 的顶点
的顶点![]() 的坐标分别是
的坐标分别是![]() ,
,![]() ,点
,点![]() 把线段
把线段![]() 三等分,延长
三等分,延长![]() 分别交
分别交![]() 于点
于点![]() ,连接
,连接![]() , 则下列结论:
, 则下列结论:![]() ;
; ![]()
![]() ③四边形
③四边形![]() 的面积为
的面积为![]() ;④
;④![]() ,其中正确的有( ).
,其中正确的有( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m+1)x+m2﹣2=0.
(1)若该方程有两个实数根,求m的最小整数值;
(2)若方程的两个实数根为x1,x2,且(x1﹣x2)2+m2=21,求m的值.
查看答案和解析>>
科目: 来源: 题型:
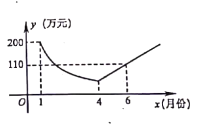
【题目】为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产并进行治污改造,其月利润![]() (万元)与月份
(万元)与月份![]() 之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的部分,下列选项错误的是( )
之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的部分,下列选项错误的是( )
A.4月份的利润为![]() 万元
万元
B.污改造完成后每月利润比前一个月增加![]() 万元
万元
C.治污改造完成前后共有![]() 个月的利润低于
个月的利润低于![]() 万元
万元
D.9月份该厂利润达到![]() 万元
万元
查看答案和解析>>
科目: 来源: 题型:
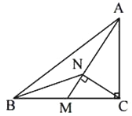
【题目】如图所示,在△ABC中,∠ACB=90°,AM是BC边的中线,CN⊥AM于N点,连接BN,求证:
(1)△MCN∽△MAC;
(2)∠NBM=∠BAM.
查看答案和解析>>
科目: 来源: 题型:
【题目】有一块两直角边长分别为AC=3cm和BC=4cm的直角三角形铁皮,要利用它来裁剪一个正方形,有两种方法:一种是正方形的一边在直角三角形的斜边上,另两个顶点在两条直角边上,如图(1);另一种是一组邻边在直角三角形的两直角边上,另一个顶点在斜边上,如图(2).用计算说明两种情形下正方形的面积哪个大?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,Rt△ABO的顶点A是双曲线y=![]() 与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=![]() .
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A.C的坐标和△AOC的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】 已知,反比例函数y=![]() 的图象和一次函数的图象交于A、B两点,点A的横坐标是-1,点B的纵坐标是-1.
的图象和一次函数的图象交于A、B两点,点A的横坐标是-1,点B的纵坐标是-1.
(1)求这个一次函数的表达式;
(2)若点P(m,n)在反比例函数图象上,且点P关于x轴对称的点Q恰好落在一次函数的图象上,求m2+n2的值;
(3)若M(x1,y1),N(x2,y2)是反比例函数在第一象限图象上的两点,满足x2-x1=2,y1+y2=3,求△MON的面积.
查看答案和解析>>
科目: 来源: 题型:
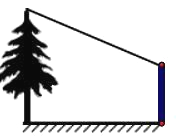
【题目】小明想测量一棵树的高度,他发现树的影子恰好落在地面和一垛墙上,如图,此时测得地面上的影长为8米,墙上的影长为4米.同一时刻,一根长为1米且垂直于地面放置的标杆在地面上的影长为2米,则树的高度为________。
查看答案和解析>>
科目: 来源: 题型:
【题目】 在正方形ABCD中.
(1)如图1,点E、F分别在BC、CD上,AE、BF相交于点O,∠AOB=90°,试判断AE与BF的数量关系,并说明理由;
(2)如图2,点E、F、G、H分别在边BC、CD、DA、AB上,EG、FH相交于点O,∠GOH=90°,且EG=7,求FH的长;
(3)如图3,点E、F分别在BC、CD上,AE、BF相交于点O,∠AOB=90°,若AB=5,图中阴影部分的面积与正方形的面积之比为4:5,求△ABO的周长.

查看答案和解析>>
科目: 来源: 题型:
【题目】 先阅读下面的材料,再解答下面的问题:如果两个三角形的形状相同,则称这两个三角形相似.如图1,△ABC与△DEF形状相同,则称△ABC与△DEF相似,记作△ABC∽△DEF.那么,如何说明两个三角形相似呢?我们可以用“两角分别相等的三角形相似”加以说明.用数学语言表示为:
如图1:在△ABC与△DEF中,∵∠A=∠D,∠B=∠E,∴△ABC∽△DEF.
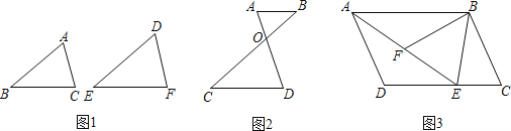
请你利用上述定理解决下面的问题:
(1)下列说法:①有一个角为50°的两个等腰三角形相似;②有一个角为100°的两个等腰三角形相似;③有一个锐角相等的两个直角三角形相似;④两个等边三角形相似.其中正确的是______(填序号);
(2)如图2,已知AB∥CD,AD与BC相交于点O,试说明△ABO∽△DCO;
(3)如图3,在平行四边形ABCD中,E是DC上一点,连接AE.F为AE上一点,且∠BFE=∠C,求证:△ABF∽△EAD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com