
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=![]() .其中正确的结论有( )
.其中正确的结论有( )
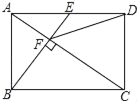
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年的暑假,李刚和他的父母计划去新疆旅游,他们打算坐飞机到乌鲁木齐,第二天租用一辆汽车自驾出游.

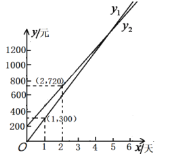
根据以上信息,解答下列问题:
(1)设租车时间为![]() 天,租用甲公司的车所需费用为
天,租用甲公司的车所需费用为![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为![]() 元,分别求出
元,分别求出![]() ,
,![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)请你帮助李刚,选择租用哪个公司的车自驾出游比较合算,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
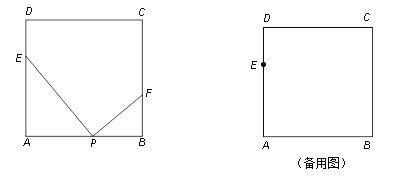
【题目】如图,在正方形ABCD中,AB=4cm,点E为AC边上一点,且AE=3cm,动点P从点A出发,以1cm/s的速度沿线段AB向终点B运动,运动时间为x s.作∠EPF=90°,与边BC相交于点F.设BF长为ycm.
(1)当x= s时,EP=PF;
(2)求在点P运动过程中,y与x之间的函数关系式;
(3)点F运动路程的长是 cm.
查看答案和解析>>
科目: 来源: 题型:
【题目】苏科版九年级下册数学课本65页有这样一道习题:
如图1,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D.
(1)△ACD与△CBD相似吗?为什么?
(2)图中还有几对相似三角形?是哪几对?
复习时,小明提出了新的发现:“利用△ACD∽△CBD∽△ABC可以进一步证明:
①CD2=ADBD,②BC2=BDAB,③AC2=ADAB.”
(1)请你按照小明的思路,选择①、②、③中的一个进行证明;
(2)小亮研究“小明的发现”时,又惊喜地发现,利用“它”可以证明“勾股定理”,请你按照小亮思路完成这个证明;
(3)小丽也由小明发现的“CD2=ADBD”,进一步发现:“已知线段a、b,可以用尺规作图作出线段c,使c2=ab”,请你完成小丽的发现.(不要求写出作法,请保留作图痕迹)
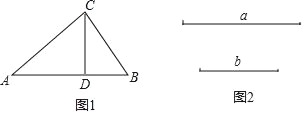
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系内,小正方形网格的边长为1个单位长度,![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() ,
,![]() ,
,![]() .
.
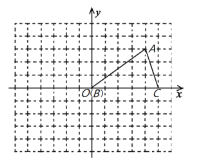
(1)画出将![]() 向上平移2个单位长度,再向左平移5个单位长度后得到的
向上平移2个单位长度,再向左平移5个单位长度后得到的![]() ;
;
(2)画出将![]() 绕点
绕点![]() 按顺时针方向旋转90°得到的
按顺时针方向旋转90°得到的![]() ;
;
(3)在![]() 轴上存在一点
轴上存在一点![]() ,满足点
,满足点![]() 到点
到点![]() 与点
与点![]() 的距离之和最小,请直接写出点
的距离之和最小,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
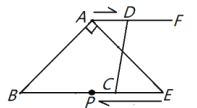
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 且点
且点![]() 在点
在点![]() 的右侧.点
的右侧.点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 方向以
方向以![]() /秒的速度运动,同时点
/秒的速度运动,同时点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 方向以
方向以![]() /秒的速度运动,在线段
/秒的速度运动,在线段![]() 上取点
上取点![]() ,使得
,使得![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() 秒.当
秒.当![]() __________秒时,以
__________秒时,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
查看答案和解析>>
科目: 来源: 题型:
【题目】某广场有一个小型喷泉,水流从垂直于地面长为1.25米的水管OA喷出,水流在各个方向上沿形状相同的抛物线路径落到地面上,某方向上抛物线路径的形状如图所示,落点B到O的距离为2.5米.建立如图直角坐标系,水流喷出的高度y(米)与水平距离x(米)之间的关系式是y=ax2+2x+c,请回答下列问题:
(1)求y与x之间的函数表达式;
(2)求水流的最大高度.

查看答案和解析>>
科目: 来源: 题型:
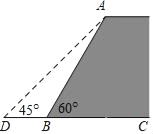
【题目】如图,一堤坝的坡角∠ABC=60°,坡面长度AB=24米(图为横截面).为了使堤坝更加牢固,需要改变堤坝的坡面,为使得坡面的坡角∠ADB=45°,则应将堤坝底端向外拓宽(BD)多少米?(结果精确到0.1米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目: 来源: 题型:
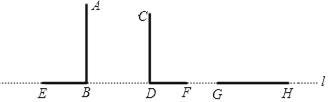
【题目】在同一水平线l上的两根竹竿AB、CD,它们在同一灯光下的影子分别为BE、DF,如图所示:(竹竿都垂直于水平线l)
(1)根据灯光下的影子确定光源S的位置;
(2)画出影子为GH的竹竿MG(用线段表示);
(3)若在点H观测到光源S的仰角是∠α,且 cosα=![]() ,GH=1.2m,请求出竹竿MG的长度.
,GH=1.2m,请求出竹竿MG的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com