
【题目】如图,在平面直角坐标系内,小正方形网格的边长为1个单位长度,![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() ,
,![]() ,
,![]() .
.
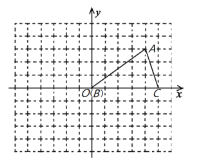
(1)画出将![]() 向上平移2个单位长度,再向左平移5个单位长度后得到的
向上平移2个单位长度,再向左平移5个单位长度后得到的![]() ;
;
(2)画出将![]() 绕点
绕点![]() 按顺时针方向旋转90°得到的
按顺时针方向旋转90°得到的![]() ;
;
(3)在![]() 轴上存在一点
轴上存在一点![]() ,满足点
,满足点![]() 到点
到点![]() 与点
与点![]() 的距离之和最小,请直接写出点
的距离之和最小,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)答案见解析;(2)答案见解析;(3)![]() .
.
【解析】
(1)先分别将A、B、C三点向上平移2个单位长度,再向左平移5个单位长度得到![]() ,然后连接
,然后连接![]() 、
、![]() 、
、![]() 即可;
即可;
(2)根据题意,先将边OC和OA绕点![]() 顺时针方向旋转90°得到
顺时针方向旋转90°得到![]() 、
、![]() ,然后连接
,然后连接![]() 即可;
即可;
(3)连接![]() 交x轴于点P,根据两点之间线段最短即可得出此时点
交x轴于点P,根据两点之间线段最短即可得出此时点![]() 到点
到点![]() 与点
与点![]() 的距离之和最小,然后利用待定系数法求出直线
的距离之和最小,然后利用待定系数法求出直线![]() 的解析式,从而求出点P 的坐标.
的解析式,从而求出点P 的坐标.
解:(1)先分别将A、B、C三点向上平移2个单位长度,再向左平移5个单位长度得到![]() ,然后连接
,然后连接![]() 、
、![]() 、
、![]() ,如图所示,
,如图所示,![]() 即为所求;
即为所求;
(2)先将边OC和OA绕点![]() 顺时针方向旋转90°得到
顺时针方向旋转90°得到![]() 、
、![]() ,然后连接
,然后连接![]() ,如图所示,
,如图所示,![]() 即为所求;
即为所求;
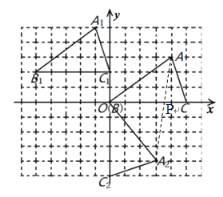
(3)连接![]() 交x轴于点P,根据两点之间线段最短,即可得出此时点
交x轴于点P,根据两点之间线段最短,即可得出此时点![]() 到点
到点![]() 与点
与点![]() 的距离之和最小,
的距离之和最小,
由平面直角坐标系可知:点A的坐标为(4,3),点![]() 的坐标为(3,-4)
的坐标为(3,-4)
设直线![]() 的解析式为y=kx+b
的解析式为y=kx+b
将A、![]() 的坐标代入,得
的坐标代入,得
![]()
解得:![]()
∴直线![]() 的解析式为y=7x-25
的解析式为y=7x-25
将y=0代入,得
![]()
∴点P的坐标为![]() .
.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】(1)把下面的证明补充完整
已知:如图,直线AB、CD被直线EF所截,AB∥CD,EG平分∠BEF,FG平分∠DFE,EG、FG交于点G.求证:EG⊥FG.
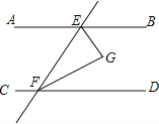
证明:∵AB∥CD(已知)
∴∠BEF+∠DFE=180°(______),
∵EG平分∠BEF,FG平分∠DFE(已知),
∴______,______(______),
∴∠GEF+∠GFE=![]() (∠BEF+∠DFE)(______),
(∠BEF+∠DFE)(______),
∴∠GEF+∠GFE=![]() ×180°=90°(______),
×180°=90°(______),
在△EGF中,∠GEF+∠GFE+∠G=180°(______),
∴∠G=180°-90°=90°(等式性质),
∴EG⊥FG(______).
(2)请用文字语言写出(1)所证命题:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材中这样写道“我们把多项式![]() 及
及![]() 这样的式子叫做完全平方式”如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法配方法是一种重要的解决数学问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决些与非负数有关的问题或求式子的最大值、最小值等.
这样的式子叫做完全平方式”如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法配方法是一种重要的解决数学问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决些与非负数有关的问题或求式子的最大值、最小值等.
例1.分解因式解:![]()
解:![]()
例2.求式子![]() 的最小值,
的最小值,
解:![]() ,
,
可知当![]() 时,
时,![]() 有最小值,最小值是
有最小值,最小值是![]() ,
,
根据以上材料用配方法解决下列问题:
![]() 在实数范围内分解因式:
在实数范围内分解因式:![]() ;
;
![]() 当
当![]() 为何值时,多项式
为何值时,多项式![]() 有最小值?并求出这个最小值.
有最小值?并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】折纸不仅可以帮助我们进行证明,还可以帮助我们进行计算.小明取了一张正方形纸片,按照如图所示的方法折叠(如图①②③):
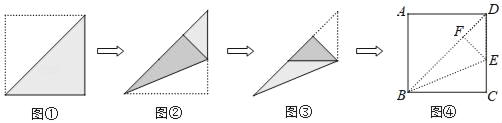
重新展开后得到如图所示的正方形ABCD(如图④),BD、BE、EF为前面折叠的折痕.小亮观察之后发现利用这个图形可以求出45°、22.5°等角的三角函数值.请你直接写出tan67.5°=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
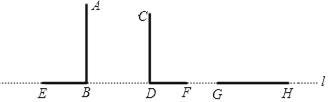
【题目】在同一水平线l上的两根竹竿AB、CD,它们在同一灯光下的影子分别为BE、DF,如图所示:(竹竿都垂直于水平线l)
(1)根据灯光下的影子确定光源S的位置;
(2)画出影子为GH的竹竿MG(用线段表示);
(3)若在点H观测到光源S的仰角是∠α,且 cosα=![]() ,GH=1.2m,请求出竹竿MG的长度.
,GH=1.2m,请求出竹竿MG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.

(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图2.
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
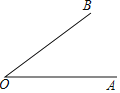
【题目】已知:![]() .
.
求作:![]() ,使得
,使得![]() .
.
作法:
①以![]() 为圆心,任意长为半径画弧,分别交
为圆心,任意长为半径画弧,分别交![]() ,
,![]() 于点
于点![]() ;
;
②画一条射线![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交
长为半径画弧,交![]() 于点
于点![]() ;
;
③以点![]() 为圆心,
为圆心,![]() 长为半径画弧,与第②步中所画的弧相交于点
长为半径画弧,与第②步中所画的弧相交于点![]() ;
;
④过点![]() 画射线
画射线![]() ,则
,则![]() .
.
根据上面的作法,完成以下问题:
(1)使用直尺和圆规,作出![]() (请保留作图痕迹).
(请保留作图痕迹).
(2)完成下面证明![]() 的过程(注:括号里填写推理的依据).
的过程(注:括号里填写推理的依据).
证明:由作法可知![]() ,
,![]() ,
,![]() ,
,
∴![]() ≌
≌![]() ( )
( )
∴![]() .( )
.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
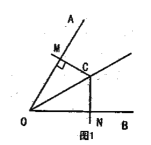
【题目】阅读材料:“直角三角形如果有一个角等于![]() ,那么这个角所对的边等于斜边的一半”,即“在
,那么这个角所对的边等于斜边的一半”,即“在![]() 中,
中,![]() ,则
,则![]() ”.利用以上知识解决下列问题:如图,已知
”.利用以上知识解决下列问题:如图,已知![]() 是
是![]() 的平分线上一点.
的平分线上一点.
(1)若![]() 与射线
与射线![]() 分别相交于点
分别相交于点![]() ,且
,且![]() .
.
①如图1,当![]() 时,求证:
时,求证: ![]() ;
;
②当![]() 时,求
时,求![]() 的值.
的值.
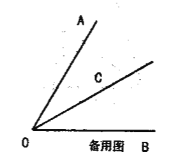
(2)若![]() 与射线
与射线![]() 的反向延长线、射线
的反向延长线、射线![]() 分别相交于点
分别相交于点![]() ,且
,且![]() ,请你直接写出线段
,请你直接写出线段![]() 三者之间的等量关系.
三者之间的等量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局为了了解学生对体育立定跳远(![]() )、跳绳(
)、跳绳(![]() )、掷实心球(
)、掷实心球(![]() )、中长跑(
)、中长跑(![]() )四个项目的喜爱程度(每人只选一项),确定中考体育考试项目,特对八年级某班进行了调查,并绘制成如下频数、频率统计表和扇形统计图:
)四个项目的喜爱程度(每人只选一项),确定中考体育考试项目,特对八年级某班进行了调查,并绘制成如下频数、频率统计表和扇形统计图:
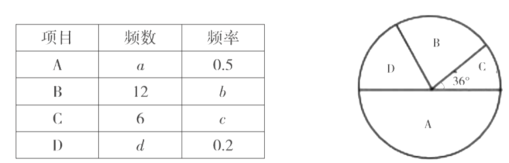
(1)求出这次调查的总人数;
(2)求出表中![]() 的值;
的值;
(3)若该校八年级有学生1200人,请你算出喜爱跳绳的人数,并发表你的看法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com