
科目: 来源: 题型:
【题目】张师傅驾车从甲地去乙地,途中在加油站加了一次油,加油时,车载电脑显示还能行驶50千米.假设加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.

(1)求张师傅加油前油箱剩余油量y(升)与行驶时间t(小时)之间的关系式;
(2)求出a的值;
(3)求张师傅途中加油多少升?
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列解题过程:
 =
= =
=![]() =
=![]() -2;
-2;
 =
= =
=![]() .
.
请回答下列问题:
(1)观察上面的解题过程,请直接写出式子![]() = ;
= ;
(2)观察上面的解题过程,请直接写出式子![]() = ;
= ;
(3)利用上面所提供的解法,请求![]() +···+
+···+![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列命题中,属于假命题的是( )
A. 有一个锐角相等的两个直角三角形一定相似
B. 对角线相等的菱形是正方形
C. 抛物线y=x2﹣20x+17的开口向上
D. 在一次抛掷图钉的试验中,若钉尖朝上的频率为![]() ,钉尖朝下的概率为
,钉尖朝下的概率为![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12 m,由此他就知道了A,B间的距离,有关他这次探究活动的描述错误的是( )

A. AB=24 m B. MN∥AB C. △CMN∽△CAB D. CM∶MA=1∶2
【答案】D
【解析】试题分析:根据三角形的中位线平行于第三边并且等于第三边的一半可得MN∥AB,MN=![]() AB,再根据相似三角形的判定解答.
AB,再根据相似三角形的判定解答.
试题解析:∵M、N分别是AC,BC的中点
∴MN∥AB,MN=![]() AB,
AB,
∴AB=2MN=2×12=24m
△CMN∽△CAB
∵M是AC的中点
∴CM=MA
∴CM:MA=1:1
故描述错误的是D选项.
故选D.
考点:1.三角形中位线定理;2.相似三角形的应用.
【题型】单选题
【结束】
10
【题目】若关于![]() 的一元二次方程
的一元二次方程![]() +x-3m=0有两个不相等的实数根,则
+x-3m=0有两个不相等的实数根,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
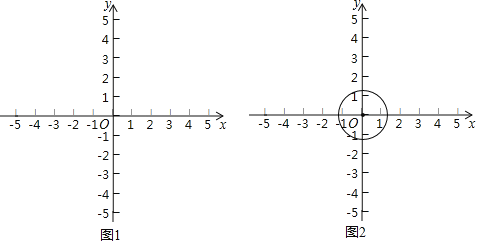
【题目】在平面直角坐标系xOy中,点M的坐标为(x1,y1),点N的坐标为(x2,y2),且x1≠x2,y1≠y2,以MN为边构造菱形,若该菱形的两条对角线分别平行于x轴,y轴,则称该菱形为边的“坐标菱形”.
(1)已知点A(1,0),B(0,![]() ),则以AB为边的“坐标菱形”的最小内角为______;
),则以AB为边的“坐标菱形”的最小内角为______;
(2)若点C(2,1),点D在直线y=5上,以CD为边的坐标菱形”为正方形,求育直线CD表达式;
(3)⊙O的半径为![]() ,点P的坐标为(3,m),若在⊙O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,求m的取值范围.
,点P的坐标为(3,m),若在⊙O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,求m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
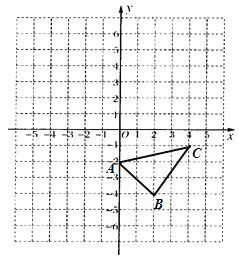
【题目】已知:如图,在平面直角坐标系中.
(1)作出△ABC关于![]() 轴对称的
轴对称的![]() ,并写出
,并写出![]() 三个顶点的坐标:
三个顶点的坐标: ![]() ( ),
( ),![]() ( ),
( ),![]() ( );
( );
(2)直接写出△ABC的面积为 ;
(3)在![]() 轴上画点P,使PA+PC最小.
轴上画点P,使PA+PC最小.
查看答案和解析>>
科目: 来源: 题型:
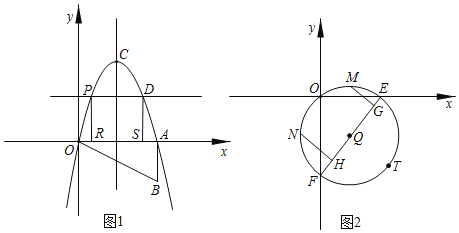
【题目】如图,Rt△OAB如图所示放置在平面直角坐标系中,直角边OA与x轴重合,∠OAB=90°,OA=4,AB=2,把Rt△OAB绕点O逆针旋转90°,点B旋转到点C的位置,一条抛物找正好经过点O,C,A三点.
(1)求该抛物线的解析式;
(2)在x轴上方的抛物线上有一动点P,过点P作x轴的平行线交抛物线于点D,分别过点P,点D作x轴的垂线,交x轴于R,S两点,问:四边形PRSD的周长是否有最大值?如果有,请求出最值,并写出解答过程;如果没有,请说明理由.
(3)如图2,把点B向下平移两个单位得到点T,过O,T两点作⊙Q交x轴,y轴于E,F两点,若M、N分别为弧![]() 、
、![]() 的中点,作MG⊥EF,NH⊥EF,垂足为G、H,试求MG+NH的值.
的中点,作MG⊥EF,NH⊥EF,垂足为G、H,试求MG+NH的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】(问题探究)
将三角形![]() 纸片沿
纸片沿![]() 折叠,使点A落在点
折叠,使点A落在点![]() 处.
处.
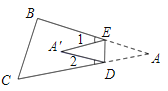
(1)如图,当点A落在四边形![]() 的边
的边![]() 上时,直接写出
上时,直接写出![]() 与
与![]() 之间的数量关系;
之间的数量关系;
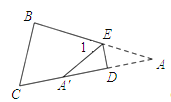
(2)如图,当点A落在四边形![]() 的内部时,求证:
的内部时,求证:![]() ;
;
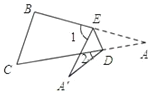
(3)如图,当点A落在四边形![]() 的外部时,探索
的外部时,探索![]() ,
,![]() ,
,![]() 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;
(拓展延伸)
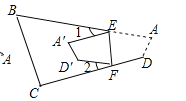
(4)如图,若把四边形![]() 纸片沿
纸片沿![]() 折叠,使点A、D落在四边形
折叠,使点A、D落在四边形![]() 的内部点
的内部点![]() 、
、![]() 的位置,请你探索此时
的位置,请你探索此时![]() ,
,![]() ,
,![]() ,
,![]() 之间的数量关系,写出你发现的结论,并说明理由.
之间的数量关系,写出你发现的结论,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
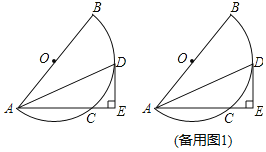
【题目】如图,AB为半圆的直径,O为半圆的圆心,AC是弦,取弧![]() 的中点D,过点D作DE⊥AC交AC的延长线于点E.
的中点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)当AB=10,AC=5时,求CE的长;
(3)连接CD,AB=10.当![]() =
=![]() 时,求DE的长.
时,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com