
科目: 来源: 题型:
【题目】如图1.△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC作等腰Rt△ABE和等腰Rt△ACF,过点E,F作射线GA的垂线,垂足分别为P,Q.
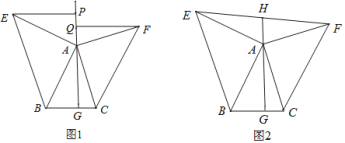
(1)求证:△EPA≌△AGB:
(2)试探究EP与FQ之间的数量关系,并证明你的结论;
(3)如图2.若连接EF交GA的延长线于H,由(2)中的结论你能判断EH与FH的大小关系吗?并说明理由:
(4)在(3)的条件下,若BC=10,AG=12.请直接写出S△AEF= .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①所示,点![]() 将线段
将线段![]() 分成两部分,如果
分成两部分,如果![]() ,那么称点
,那么称点![]() 为线段
为线段![]() 的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线将一个面积为
的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线将一个面积为![]() 的图形分成两部分,这两部分的面积分别为
的图形分成两部分,这两部分的面积分别为![]() ,
,![]() ,如果
,如果![]() ,那么称直线为该图形的黄金分割线.
,那么称直线为该图形的黄金分割线.
问题探究:
(1)研究小组猜想:在![]() 中,若点
中,若点![]() 为
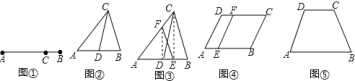
为![]() 上的黄金分割点,如图②,则直线
上的黄金分割点,如图②,则直线![]() 是
是![]() 的黄金分割线,你认为呢?为什么?
的黄金分割线,你认为呢?为什么?
(2)研究小组在进一步探究中发现:过点![]() 任作一条直线交
任作一条直线交![]() 于点
于点![]() ,再过点
,再过点![]() 作直线
作直线![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() 如图③,则直线
如图③,则直线![]() 也是
也是![]() 的黄金分割线,请你说明理由.
的黄金分割线,请你说明理由.
(3)如图④,点![]() 是平行四边形
是平行四边形![]() 的边
的边![]() 的黄金分割点,过点
的黄金分割点,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,显然直线
,显然直线![]() 是平行四边形的黄金分割线,请你画一条平行四边形
是平行四边形的黄金分割线,请你画一条平行四边形![]() 的黄金分割线,使它不经过四边形
的黄金分割线,使它不经过四边形![]() 各边黄金分割点.
各边黄金分割点.
(4)如图⑤等腰梯形![]() ,请你画出它的一条黄金分割线,使它不经过各边的黄金分割点.
,请你画出它的一条黄金分割线,使它不经过各边的黄金分割点.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,点
,点![]() 、
、![]() 为直线
为直线![]() 上的两动点,
上的两动点,![]() ,
,![]() ,
,![]() ;
;
(1)当点![]() 、
、![]() 重合,即
重合,即![]() 时(如图
时(如图![]() ),试求
),试求![]() .(用含
.(用含![]() ,
,![]() ,
,![]() 的代数式表示)
的代数式表示)
(2)请直接应用(1)的结论解决下面问题:当![]() 、
、![]() 不重合,即
不重合,即![]() ,
,
①如图![]() 这种情况时,试求
这种情况时,试求![]() .(用含
.(用含![]() ,
,![]() ,
,![]() ,
,![]() 的代数式表示)
的代数式表示)
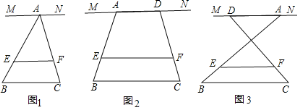
②如图![]() 这种情况时,试猜想
这种情况时,试猜想![]() 与
与![]() 、
、![]() 之间有何种数量关系?并证明你的猜想.
之间有何种数量关系?并证明你的猜想.
查看答案和解析>>
科目: 来源: 题型:
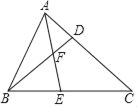
【题目】如图,已知点D、E分别在△ABC的边AC、BC上,线段BD与AE交于点F,且CDCA=CECB.
(1)求证:∠CAE=∠CBD;
(2)若![]() ,求证:ABAD=AFAE.
,求证:ABAD=AFAE.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价均为4000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一台按原价收费,其余每台优惠25%;乙商场的优惠条件是:每台优惠20%.
(1)设该学校所买的电脑台数是x台,选择甲商场时,所需费用为![]() 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为![]() 元,请分别写出
元,请分别写出![]() ,
, ![]() 与x之间的关系式;
与x之间的关系式;
(2)该学校如何根据所买电脑的台数选择到哪间商场购买,所需费用较少?
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△AB1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去……,若点A(![]() ,0),B(0,2).则点B2019的坐标是( )
,0),B(0,2).则点B2019的坐标是( )
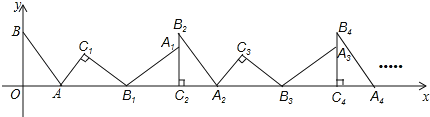
A.(6052,0)B.(6054,2)C.(6058,0)D.(6060,2)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论,①△BDF是等腰三角形;②DE=BD+CE;③若∠A=50°,∠BFC=105°;④BF=CF.其中正确的有( )
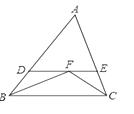
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com