【题目】如图，△ABC中，∠ABC与∠ACB的平分线交于点F，过点F作DE∥BC交AB于点D，交AC于点E，那么下列结论，①△BDF是等腰三角形；②DE＝BD+CE；③若∠A＝50°，∠BFC＝105°；④BF＝CF．其中正确的有（ ）
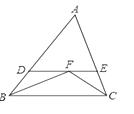
A.1个B.2个C.3个D.4个
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，已知AD=AE，添加下列条件仍无法证明△ABE≌△ACD的是 （ ）
A. AB=AC B. ∠ADC=∠AEB C. ∠B=∠C D. BE=CD
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形纸片ABCD中，已知AD =8，折叠纸片使AB边与对角线AC
重合，点B落在点F处，折痕为AE，且EF=3，则AB的长为( )
A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（问题背景）解方程：x4﹣5x2+4=0．
这是一个一元四次方程，根据该方程的特点，我们可以借助“换元法”将高次方程“降次”，进而解得未知数的值．
解：设 x2=y，那么 x4=y2，于是原方程可变为 y2﹣5y+4=0，解得 y1=1，y2=4． 当 y1=1 时，x2=1，x=±1；当 y2=4 时，x2=4，x=±2；
原方程有四个根：x1=1，x2=﹣1，x3=2，x4=﹣2．
（触类旁通）参照例题解方程：（x2+x）2﹣4（x2+x）﹣12=0；
（解决问题）已知实数 x，y 满足（2x+2y+3）（2x+2y﹣3）=27，求 x+y 的值；
（拓展迁移）分解因式：（x2+4x+3）（x2+4x+5）+1．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知
，点
、
为直线
上的两动点，
，
，
；
（1）当点、重合，即
时（如图
），试求
．（用含
，
，
的代数式表示）
（2）请直接应用（1）的结论解决下面问题：当、不重合，即
，
①如图
这种情况时，试求．（用含
，，，的代数式表示）
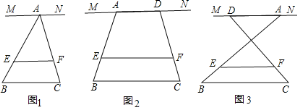
②如图
这种情况时，试猜想与、之间有何种数量关系？并证明你的猜想．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点
若点D为BC边的中点，点M为线段EF上一动点，则
周长的最小值为
A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学八⑴班、⑵班各选5名同学参加“爱我中华”演讲比赛，其预赛成绩（满分100分）如图所示：
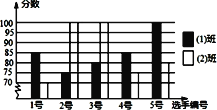
（1）根据上图填写下表：
平均数 | 中位数 | 众数 | |
八（1）班 | 85 | 85 | |
八（2）班 | 85 | 80 |
（2）根据两班成绩的平均数和中位数，分析哪班成绩较好？
（3）如果每班各选2名同学参加决赛，你认为哪个班实力更强些？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某快餐连锁店招聘外卖骑手，并提供了如下两种日工资方案：
方案一：每日底薪60元，每完成一单快递业务再提成3元；
方案二：每日底薪100元，快递业务的前40单没有提成，从第41单开始，每完成一单快递业务再提成5元．
设骑手每日完成的快递业务量为n（n为正整数，单位：单），方案一，二中骑手的日工资分别为y1，y2（单位：元）．
（1）分别写出y1，y2关于n的函数解析式；
（2）据统计，新聘骑手小文上班第一周每日完成的快递业务量的平均数约为60单．若仅从日工资收入的角度考虑，他应该选择哪种日工资方案？请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
