
【题目】已知等边![]() 边长为
边长为![]() ,
,![]() 、
、![]() 分别为
分别为![]() 和
和![]() 上的点,且
上的点,且![]() ,则
,则![]() ________度;若点
________度;若点![]() 为
为![]() 的三等分点,则
的三等分点,则![]() ________.
________.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A.0.350是精确到0.001的近似数
B.3.80万是精确到百位的近似数
C.一个鸡蛋的质量为50.47g,用四舍五入法将50.47精确到0.1的近似值为51.0
D.近似数2.20是由数![]() 四舍五入得到的,那么数
四舍五入得到的,那么数![]() 的取值范围是
的取值范围是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80米的围网在水库中围成发如图所示①②③的三块矩形区域,而且这三块矩形区域面积相等.已知矩形区域ABCD的面积为30m2,设BC的长度为xm,所列方程为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,弦AD,BC相交于点E,连接OE,已知AD=BC,AD⊥CB.
(1)求证:AB=CD;
(2)如果⊙O的直径为10,DE=1,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
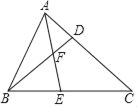
【题目】如图,已知点D、E分别在△ABC的边AC、BC上,线段BD与AE交于点F,且CDCA=CECB.
(1)求证:∠CAE=∠CBD;
(2)若![]() ,求证:ABAD=AFAE.
,求证:ABAD=AFAE.
查看答案和解析>>
科目:初中数学 来源: 题型:
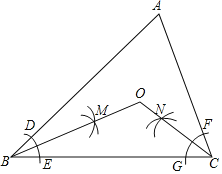
【题目】如图,在△ABC中,∠A=70°.按下列步骤作图:①分别以点B,C为圆心,适当长为半径画弧,分别交BA,BC,CA,CB于点D,E,F,G;②分别以点D,E为圆心,大于![]() DE为半径画弧,两弧交于点M;③分别以点F,G为圆心,大于
DE为半径画弧,两弧交于点M;③分别以点F,G为圆心,大于![]() FG为半径画弧,两弧交于点N;④作射线BM交射线CN于点O.则∠BOC的度数是_____.
FG为半径画弧,两弧交于点N;④作射线BM交射线CN于点O.则∠BOC的度数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
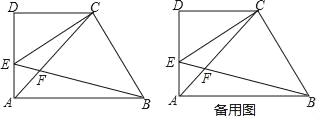
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
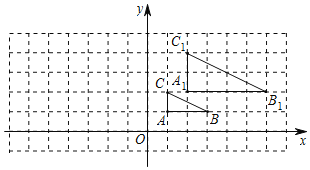
【题目】如图,在平面直角坐标系网格中,将△ABC进行位似变换得到△A1B1C1.
(1)△A1B1C1与△ABC的位似比是______.
(2)画出△A1B1C1关于y轴对称的△A2B2C2.
(3)若点B的坐标为(3,1)为△ABC内一点,则依上述两次变换后,点B2的坐标是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com