
科目: 来源: 题型:
【题目】在一个不透明的口袋里有分别标注2、4、6的3个小球(小球除数字不同外,其余都相同),另有3张背面完全一样、正面分别写有数字6、7、8的卡片.现从口袋中任意摸出一个小球,再从这3张背面朝上的卡片中任意摸出一张卡片.
(1)请你用列表或画树状图的方法,表示出所有可能出现的结果;
(2)小红和小莉做游戏,制定了两个游戏规则:
规则1:若两次摸出的数字,至少有一次是“6”,小红赢;否则,小莉赢.
规则2:若摸出的卡片上的数字是球上数字的整数倍时,小红赢;否则,小莉赢.
小红要想在游戏中获胜,她会选择哪一种规则,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
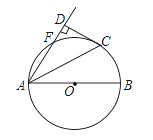
【题目】如图,AB是⊙O的直径,点F、C在⊙O上且![]() , 连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.
, 连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.
(1)求证:CD是⊙O的切线;
(2)若![]() , CD=4,求⊙O的半径.
, CD=4,求⊙O的半径.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲班56人,其中身高在160厘米以上的男同学10人,身高在160厘米以上的女同学3人,乙班80人,其中身高在160厘米以上的男同学20人,身高在160厘米以上的女同学8人.如果想在两个班的160厘米以上的女生中抽出一个作为旗手,在哪个班成功的机会大?为什么?
查看答案和解析>>
科目: 来源: 题型:
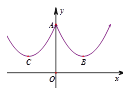
【题目】如图4所示的是桥梁的两条钢缆具有相同的抛物线形状.按照图中建立的直角坐标系,右面的一条抛物线的解析式为y=x2-4x+5表示,而且左右两条抛物线关于y轴对称,则左面钢缆的表达式为_________________________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料:
如图![]() ,把
,把![]() 沿直线
沿直线![]() 平行移动线段
平行移动线段![]() 的长度,可以变到
的长度,可以变到![]() 的位置;
的位置;
如图![]() ,以
,以![]() 为轴,把
为轴,把![]() 翻折
翻折![]() ,可以变到
,可以变到![]() 的位置;
的位置;
如图![]() ,以点
,以点![]() 为中心,把
为中心,把![]() 旋转
旋转![]() ,可以变到
,可以变到![]() 的位置.
的位置.
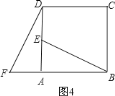
像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的.这种只改变位置,不改变形状大小的图形变换,叫做三角形的全等变换.
回答下列问题:
①在图![]() 中,可以通过平行移动、翻折、旋转中的哪一种方法怎样变化,使
中,可以通过平行移动、翻折、旋转中的哪一种方法怎样变化,使![]() 变到
变到![]() 的位置;
的位置;
②指图中线段![]() 与
与![]() 之间的关系,为什么?
之间的关系,为什么?

查看答案和解析>>
科目: 来源: 题型:
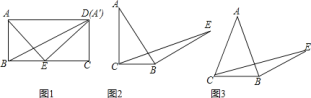
【题目】问题原型:如图①,在矩形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边中点,将线段
边中点,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,易得
,易得![]() 的面积为
的面积为![]() .
.
初步探究:如图②,在![]() 中,
中,![]() ,
,![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到线段
,得到线段![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() 的面积,并说明理由.
的面积,并说明理由.
简单应用:如图③,在等腰三角形![]() 中,
中,![]() ,
,![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,直接写出
,直接写出![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,把一个直角三角尺![]() 绕着
绕着![]() 角的顶点
角的顶点![]() 顺时针旋转,使得点
顺时针旋转,使得点![]() 与
与![]() 的延长线上的点
的延长线上的点![]() 重合,已知
重合,已知![]() .
.
(1)三角尺旋转了多少度?连结![]() ,试判断
,试判断![]() 的形状;
的形状;
(2)求![]() 的长;
的长;
(3)边结![]() ,试猜想线段
,试猜想线段![]() 与
与![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.

查看答案和解析>>
科目: 来源: 题型:
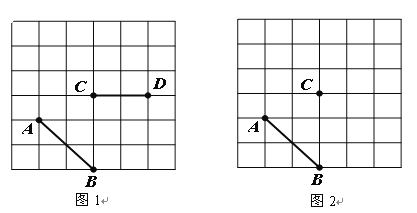
【题目】如图,正方形网格中,小格的顶点叫做格点,连接任意两个格点的线段叫做格点线段。
(1)如图1,格点线段AB、CD,请添加一条格点线段EF,使它们构成轴对称图形;
(2)如图2,格点线段AB和格点C,在网格中找一格点D,使格点A、B、C、D四点构成中心对称图形;
(3)在(2)的条件下,如果每一小正方形边长为1,那么四边形ABCD的面积S为_________.
(请直接填写)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com