【题目】AD是等腰△ABC中BC边上的高，且AD＝BC，请通过画图求出∠ABC所有可能的值．

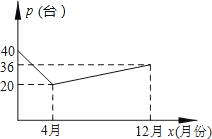
【题目】由于国家重点扶持节能环保产业，某种节能产品的销售市场逐渐回暖，某经销商销售这种产品，年初与生产厂家签订了一份进货合同，约定一年内进价为0.1万元/台．若一年内该产品的售价y（万元/台）与月份x（1≤x≤12且为整数）满足关系式：y＝，一年后，发现这一年来实际每月的销售量p（台）与月份x之间存在如图所示的变化趋势．

（1）求实际每月的销售量p（台）与月份x之间的函数表达式；

（2）全年中哪个月份的实际销售利润w最高，最高为多少万元？

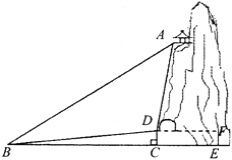
（1）求∠ADB的度数：

（2）过D点作AB的垂线，垂足为G，求DG的长及索道AB的长．（结果保留根号）

请你根据统计图解答下列问题：

（1）在这次调查中一共抽查了__________名学生，其中，喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为__________，喜欢“戏曲”活动项目的人数是__________人；

（2）若在“舞蹈、乐器、声乐、戏曲”活动项目任选两项设立课外兴趣小组，请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项活动的概率．

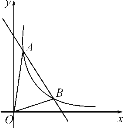
【题目】如图，一次函数y＝kx＋b与反比例函数y＝(x>0)的图象交于A(m，6)，B(3，n)两点．

(1) 求一次函数的表达式；

(2) 根据图象写出kx＋b－<0的x的取值范围．

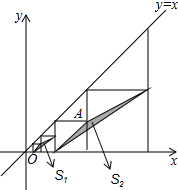
【题目】如图，在平面直角坐标系中，边长不等的正方形依次排列，每个正方形都有一个顶点落在函数的图象上，从左向右第3个正方形中的一个顶点A的坐标为，阴影三角形部分的面积从左向右依次记为、、、、，则的值为______用含n的代数式表示，n为正整数

【题目】将沿弦BC折叠，交直径AB于点D，若AD＝4，DB＝5，则BC的长是（　　）

A. 3 B. 8 C. D. 2

【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示，对称轴为直线.下列结论中，正确的是（　　）

A. abc>0 B. a+b=0 C. 2b+c>0 D. 4a+c<2b

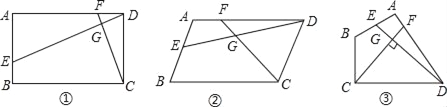
（1）如图①，若AB∥CD，AB＝CD，∠A＝90°，且ADDF＝AEDC，求证：DE⊥CF：

（2）如图②，若AB∥CD，AB＝CD，且∠A＝∠EGC时，求证：DECD＝CFDA：

（3）如图③，若BA＝BC＝3，DA＝DC＝4，设DE⊥CF，当∠BAD＝90°时，试判断是否为定值，并证明．