
科目: 来源: 题型:
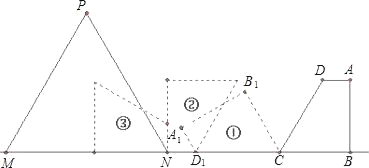
【题目】如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,BC=5,CD=6,∠DCB=60°,等边△PMN(N为固定点)的边长为x,边MN在直线BC上,NC=8.将直角梯形ABCD绕点C按逆时针方向旋转到①的位置,再绕点D1按逆时针方向旋转到②的位置,如此旋转下去.
(1)将直角梯形按此方法旋转四次,如果等边△PMN的边长为x≥5+3![]() ,求梯形与等边三角形的重叠部分的面积;
,求梯形与等边三角形的重叠部分的面积;
(2)将直角梯形按此方法旋转三次,如果梯形与等边三角形的重叠部分的面积是![]() ,求等边△PMN的边长x的范围.
,求等边△PMN的边长x的范围.
(3)将直角梯形按此方法旋转三次,如果梯形与等边三角形的重叠部分的面积是梯形面积的一半,求等边△PMN的边长x.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市高铁站将于今年年底使用,计划在广场内种植A、B两种花木共2000棵,若种植A种花木的数量比种植B种花木数量的3倍多400棵.
(1)求种植A、B两种花木的数量分别是多少棵?
(2)如果园林处安排12人同时种植这两种花木,每人每天能种植A种花木40棵或B种花木30棵,应分别安排多少人种植A种花木和B种花木,才能确保同时完成各自的任务?
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔 试 | 面 试 | 体 能 | |
甲 | 85 | 80 | 75 |
乙 | 80 | 90 | 73 |
丙 | 83 | 79 | 90 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分(不计其他因素条件),请你说明谁将被录用.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,反比例函数y=![]() 的图象过点A(1,3),请根据下列条件试用无刻度的直尺分别在图1和图2中按要求画图.
的图象过点A(1,3),请根据下列条件试用无刻度的直尺分别在图1和图2中按要求画图.
(1)在图1中取一点B,使其坐标为(﹣1,﹣3);
(2)在图2中,在(1)中画图的基础上,画一个平行四边形ACBD.

查看答案和解析>>
科目: 来源: 题型:
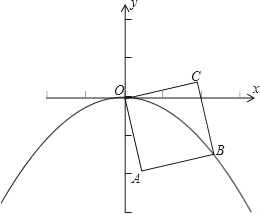
【题目】如图,OABC是边长为1的正方形,OC与x轴正半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为( )
A. ![]() B.
B. ![]() C. ﹣2 D.
C. ﹣2 D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一艘轮船在A处测得灯塔P位于其东北方向上,轮船沿正东方向航行30海里到达B处后,此时测得灯塔P位于其北偏东30°方向上,此时轮船与灯塔P的距离是( )海里.

A. 15![]() +15 B. 30
+15 B. 30![]() +30 C. 45+15
+30 C. 45+15![]() D. 60
D. 60
查看答案和解析>>
科目: 来源: 题型:
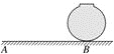
【题目】如图是置于水平地面上的一个球形储油罐,小敏想测量它的半径、在阳光下,他测得球的影子的最远点A到球罐与地面接触点B的距离是10米(如示意图,AB=10米);同一时刻,他又测得竖直立在地面上长为1米的竹竿的影子长为2米,那么,球的半径是________米.
查看答案和解析>>
科目: 来源: 题型:
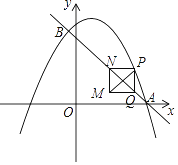
【题目】如图,在平面直角坐标系中,直线y=﹣x+3与抛物线![]() 交于A、B两点,点A在x轴上,点B的横坐标为
交于A、B两点,点A在x轴上,点B的横坐标为![]() .动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
.动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
(1)求b、c的值.
(2)当点N落在直线AB上时,直接写出m的取值范围.
(3)当点P在A、B两点之间的抛物线上运动时,设正方形PQMN的周长为C,求C与m之间的函数关系式,并写出C随m增大而增大时m的取值范围.
(4)当△PQM与坐标轴有2个公共点时,直接写出m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com