
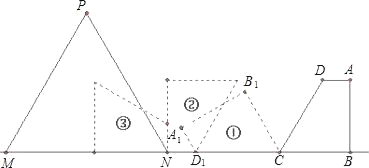
【题目】如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,BC=5,CD=6,∠DCB=60°,等边△PMN(N为固定点)的边长为x,边MN在直线BC上,NC=8.将直角梯形ABCD绕点C按逆时针方向旋转到①的位置,再绕点D1按逆时针方向旋转到②的位置,如此旋转下去.
(1)将直角梯形按此方法旋转四次,如果等边△PMN的边长为x≥5+3![]() ,求梯形与等边三角形的重叠部分的面积;
,求梯形与等边三角形的重叠部分的面积;
(2)将直角梯形按此方法旋转三次,如果梯形与等边三角形的重叠部分的面积是![]() ,求等边△PMN的边长x的范围.
,求等边△PMN的边长x的范围.
(3)将直角梯形按此方法旋转三次,如果梯形与等边三角形的重叠部分的面积是梯形面积的一半,求等边△PMN的边长x.
【答案】(1)S重叠部分=![]() ;(2)等边△PMN的边长x的范围为:x≥
;(2)等边△PMN的边长x的范围为:x≥![]() ;(3)等边三角形的边长为:
;(3)等边三角形的边长为:![]() ﹣2
﹣2![]() .
.
【解析】
(1)解本题要先判断出转2次后A点与N点的距离,根据题意,转2次的路程应该是CD+AD,如果过D作DF⊥BC,那么AD=BF=BC-CF,在直角三角形DCF中,CF=3,DF=3![]() ,因此AD=2那么转动两次后的路程是6+2=8,因此转动两次后A,N两点是重合的,那么再看第三次和第四次转动的长度,即AB+BC的长,为5+3
,因此AD=2那么转动两次后的路程是6+2=8,因此转动两次后A,N两点是重合的,那么再看第三次和第四次转动的长度,即AB+BC的长,为5+3![]() ,那么根据题意可知,梯形完全在等边三角形内,因此重合部分的面积其实就是梯形的面积.根据梯形的面积计算方法和已知的数据即可求出梯形的面积.
,那么根据题意可知,梯形完全在等边三角形内,因此重合部分的面积其实就是梯形的面积.根据梯形的面积计算方法和已知的数据即可求出梯形的面积.
(2)本题的关键是要判断出旋转3次后哪些是重合部分,如果设旋转3次后PN与DC交于N,那么先要求出四边形CBNK的面积是多少,如果四边形的面积大于![]() ,则说明四边形CBNK只有部分在等边三角形内,如果四边形的面积等于
,则说明四边形CBNK只有部分在等边三角形内,如果四边形的面积等于![]() ,就说明四边形CBNK全部在等边三角形内,这点对判断等边三角形的边长的取值范围至关重要.那么先求四边形CBNK的面积.由于四边形的面积=梯形的面积-三角形NKD的面积,那么关键是求出三角形NDK的面积,已知了三角形的底边ND的长,可过K作ND边上的高KH,那么直角三角形NKH中,∠KNH=30°,∠NDK=120°,由此可得出∠HKD=∠HDK=30°,KD=AD=2,那么可求出DH,KH的长,也就求出了三角形NDK的面积,进而可得出四边形CBNK的面积为
,就说明四边形CBNK全部在等边三角形内,这点对判断等边三角形的边长的取值范围至关重要.那么先求四边形CBNK的面积.由于四边形的面积=梯形的面积-三角形NKD的面积,那么关键是求出三角形NDK的面积,已知了三角形的底边ND的长,可过K作ND边上的高KH,那么直角三角形NKH中,∠KNH=30°,∠NDK=120°,由此可得出∠HKD=∠HDK=30°,KD=AD=2,那么可求出DH,KH的长,也就求出了三角形NDK的面积,进而可得出四边形CBNK的面积为![]() ,由此可得出四边形CBNK全部在等边三角形内,那么可通过计算此时等边三角形的边长最小的情况来得出等边三角形的边长的取值范围,过C作PM的平行线EG,然后在上下两个直角三角形中分别求出CE和CG,那么EG就是等边三角形边长的最小值,由此可得出等边三角形的边长的取值范围.
,由此可得出四边形CBNK全部在等边三角形内,那么可通过计算此时等边三角形的边长最小的情况来得出等边三角形的边长的取值范围,过C作PM的平行线EG,然后在上下两个直角三角形中分别求出CE和CG,那么EG就是等边三角形边长的最小值,由此可得出等边三角形的边长的取值范围.
(3)本题要先判断等边三角形边长的大致范围,因为这影响到重合部分的面积的计算方法,可过B作PM的平行线BK,过E作PM的平行线EG交CD于H,那么要先判断四边形BHEN的面积是否是梯形面积的一半,也就是求三角形BHC和NDE的面积和是否为梯形面积的一半,我们可求的两三角形的面积和小于梯形的面积的一半,那么等边三角形的PM边必在BK与GE中间,那么我们设这边为RK还是交CD于H,那么可先求出三角形GEN的面积,然后可根据GEN与RNH相似,用相似比表示出三角形RNH的面积,然后再求出三角形HKE的面积,这样四边形RHEN的面积=三角形RNH的面积-三角形HKE的面积=梯形的面积的一半,由此可得出关于x的方程,求出x的值即可.
解:(1)过点D作DF⊥BC,垂足为F,

∵CD=6,∠DCB=60°,
∴∠CDF=30°,
∴CF=![]() =3,DF=3
=3,DF=3![]() ,
,
∴BF=BC﹣CF=2,
又∵梯形ABCD为直角梯形,
∴∠A=∠B=90°而∠DFB=90°,
∴四边形ABFD为矩形,
∴AD=BF=2,
∴A2D1+D1C=2+6=8,
又∵NC=8,
∴点N与A2重合,
∵C4N=B3C4+B3N=5+3![]() ,
,
又∵MN>5+3![]() ,
,
∴直角梯形与等边三角形的重叠部分即为整个直角梯形,
∴S重叠部分=![]() .
.
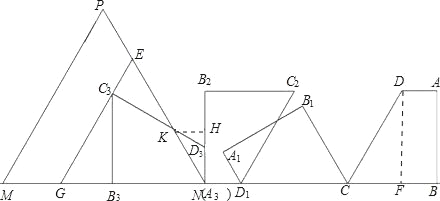
(2)过点C3作GE∥MP交MN于点G,交NP于占E,
则△GNE为等边三角形,
过点K作KH⊥B2N,垂足为H,
在Rt△NKH中∠KNH=30°,∠ND3K=120°,
∴∠KNH=∠NKD3,
∴ND3=D3K=2,
∴D3H=1,KH=![]() ,
,
∴S△D3KH=![]() ,
,
而S梯形=![]() ,
,
∴S梯形﹣S△ND3K=![]() ﹣
﹣![]() =
=![]() =重叠部分面积,
=重叠部分面积,
在Rt△GC3B3中,∠GC3B3=30°,C3B3=5,
∴GC3=![]() ,
,
C3K=C3D3﹣D3K=6﹣2=4,
C3E=C3Ktan30°=4×![]() ,
,
∴GE=GC3+C3E=![]() ,
,
∴等边△PMN的边长x的范围为:x≥![]() ,
,
(3)如图:GE∥B3K∥PM,
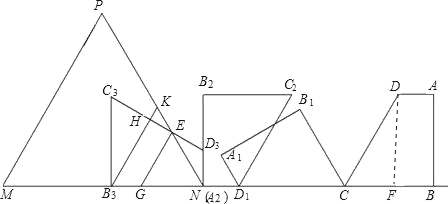
Rt△B3C3H中,B3C3=5,∠C3=30°,
∴Rt△B3C3H的面积为:![]() ,
,
∴Rt△B3C3H的面积+△D3NE的面积=![]() (梯形面积的一半),
(梯形面积的一半),
等边三角形的一边RK应落在GE与B3K之间,如图所示,

等边△GNE的边长为2![]() ,面积为3
,面积为3![]() ,
,
∵GE∥RK,
∴△GNE∽△RNK,
∴S△GNE:S△RNK=(NE:NK)2,
设KE=x,则S△GNE:S△RNK=(![]() )2,
)2,
而四边形RNEH的面积为梯形的面积的一半,即![]() ,
,
在△HEK中,KE=x,∠KEH=30°,
∴S△KEH=![]() ,
,
∴S△NRK=![]() ,
,
∴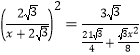 ,
,
∴x=![]() ,
,
∴x=![]() (负值舍去),
(负值舍去),
RN=NE+EK=![]() ,
,
即此时等边三角形的边长为:![]() .
.


科目:初中数学 来源: 题型:
【题目】同学们,在我们进入高中以后,将还会学到下面三角函数公式:
sin (α-β)=sinαcosβ-cosαsinβ,
cos (α-β)=cosαcosβ+sinαsinβ
例:sin 15°=sin (45°-30°)=sin 45°cos 30°-cos 45°sin 30°=![]()
(1)试仿照例题,求出cos 15°的准确值;
(2)我们知道,tanα=![]() ,试求出tan 15°的准确值.
,试求出tan 15°的准确值.
查看答案和解析>>
科目:初中数学 来源: 题型:
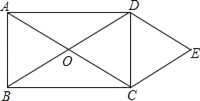
【题目】如图所示,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=3,BC=4,求四边形OCED的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
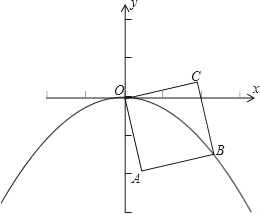
【题目】如图,OABC是边长为1的正方形,OC与x轴正半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为( )
A. ![]() B.
B. ![]() C. ﹣2 D.
C. ﹣2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
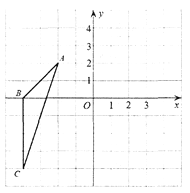
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-2,2),B(-4,0),C(-4;-4),
(1)在y轴右侧,以O为位似中心,画出△A'B'C′,使它与△ABC的相似比为1:2;
(2)根据(1)的作图,sin∠A'C'B′=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
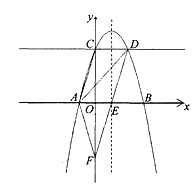
【题目】如图,在平面直角坐标系中,—抛物线y=﹣a(x+1)(x﹣3)(a>0)与x轴交于A、B两点,与y轴交于点C.抛物线的对称轴与x轴交于点E,过点C作x轴的平行线,与抛物线交于点D,连接DE,延长DE交y轴于点F,连接AD、AF.
(1)点A的坐标为____________,点B的坐标为_________ ;
(2)判断四边形ACDE的形状,并给出证明;
(3)当a为何值时,△ADF是直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
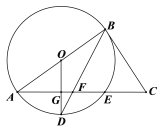
【题目】如图,在⊙O中,AB是⊙O的直径,AE是弦,OG⊥AE于点G,交⊙O 于点D,连结BD交AE于点F,延长AE至点C,连结BC.
(1)当BC=FC时,证明:BC是⊙O的切线;
(2)已知⊙O的半径![]() ,当tanA=
,当tanA=![]() ,求GF的长.
,求GF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场,为了吸引顾客,在“白色情人节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 18 | 24 | 18 |
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.
(2)如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼品券,请你帮助分析选择哪种方案较为实惠.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com