
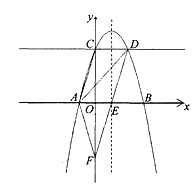
【题目】如图,在平面直角坐标系中,—抛物线y=﹣a(x+1)(x﹣3)(a>0)与x轴交于A、B两点,与y轴交于点C.抛物线的对称轴与x轴交于点E,过点C作x轴的平行线,与抛物线交于点D,连接DE,延长DE交y轴于点F,连接AD、AF.
(1)点A的坐标为____________,点B的坐标为_________ ;
(2)判断四边形ACDE的形状,并给出证明;
(3)当a为何值时,△ADF是直角三角形?
【答案】(1)点A(﹣1,0),点B(3,0);(2)四边形ACDE是平行四边形.证明见解析;(3)当![]() 或
或![]() 时,△ADF为直角三角形.
时,△ADF为直角三角形.
【解析】
(1)根据抛物线的解析式可知当y=0时,x=﹣1或x=3,即可得解;
(2)由(1)可得抛物线对称轴为直线x=1,根据抛物线图象性质易得AE=CD=2,又因为![]() ,所以四边形ACDE是平行四边形;
,所以四边形ACDE是平行四边形;
(3)过点D作DG⊥AB于点G,通过“角边角”易证△OEF ≌△DEG,OF=GD=3a,即F点坐标为(0,-3a),①若∠DAF=90°,则∠DAG+∠FAO=90°,然后证明△AOF∽△DGA,得到![]() ,然后求得符合题意的a即可;②若∠DFA=90°,则∠DFC+∠AFO=90°,易得OF垂直平分AE,AF=EF,则∠DFC=∠AFO=45°,所以OF=OA,即
,然后求得符合题意的a即可;②若∠DFA=90°,则∠DFC+∠AFO=90°,易得OF垂直平分AE,AF=EF,则∠DFC=∠AFO=45°,所以OF=OA,即![]() ,a=
,a=![]() .
.
解(1)根据题意可知,
∵y=﹣a(x+1)(x﹣3),
∴当y=0时,x=﹣1或x=3,
∴点A(﹣1,0),点B(3,0);
(2)四边形ACDE是平行四边形.
证明如下:令![]() ,得
,得![]() ,即
,即![]() ,
,
∵点A(﹣1,0),B(3,0),
∴抛物线的对称轴为直线x=1,
∴点D(2,3a),E(1,0),
∴AE=CD=2,
又![]() ,
,
∴四边形ACDE是平行四边形;
(3)过点D作DG⊥AB于点G,由![]() ,可知OE=GE,
,可知OE=GE,
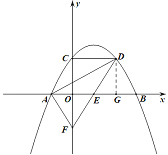
又∵∠FOE=∠DGE=90°,∠OEF=∠GED,
∴△OEF ≌△DEG(ASA),
∴OF=GD=3a,
∴F点坐标为(0,-3a),
讨论:①若∠DAF=90°,则∠DAG+∠FAO=90°,
又∠FAO+∠AFO=90°,
∴∠DAG=∠AFO,
又∠AOF=∠DGA=90°,
∴△AOF∽△DGA,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
∵a > 0,
∴![]() ,
,
∵以上各步均可逆,故![]() 合题意;
合题意;
②若∠DFA=90°,则∠DFC+∠AFO=90°,
又∵![]() ,
,
∴OF垂直平分AE,
∴AF=EF,
∴∠DFC=∠AFO=45°,
∴OF=OA,
∴![]() ,
,
∴![]() ,
,
∵以上各步均可逆,故![]() 合题意.
合题意.
综上,当![]() 或
或![]() 时,△ADF为直角三角形.
时,△ADF为直角三角形.


科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图①,正方形AEFG的两边分别在正方形ABCD的边AB和AD上,连接CF.
①写出线段CF与DG的数量关系;
②写出直线CF与DG所夹锐角的度数.
(2)拓展探究:
如图②,将正方形AEFG绕点A逆时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请利用图②进行说明.
(2)问题解决
如图③,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=4,O为AC的中点.若点D在直线BC上运动,连接OE,则在点D的运动过程中,线段OE的长的最小值.(直接写出结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件获利减少2元.设每天安排x人生产乙产品.
(1)根据信息填表
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | 15 | ||
乙 |
|
|
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元,求每件乙产品可获得的利润.
(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润W(元)的最大值及相应的x值.
查看答案和解析>>
科目:初中数学 来源: 题型:
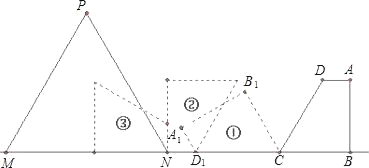
【题目】如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,BC=5,CD=6,∠DCB=60°,等边△PMN(N为固定点)的边长为x,边MN在直线BC上,NC=8.将直角梯形ABCD绕点C按逆时针方向旋转到①的位置,再绕点D1按逆时针方向旋转到②的位置,如此旋转下去.
(1)将直角梯形按此方法旋转四次,如果等边△PMN的边长为x≥5+3![]() ,求梯形与等边三角形的重叠部分的面积;
,求梯形与等边三角形的重叠部分的面积;
(2)将直角梯形按此方法旋转三次,如果梯形与等边三角形的重叠部分的面积是![]() ,求等边△PMN的边长x的范围.
,求等边△PMN的边长x的范围.
(3)将直角梯形按此方法旋转三次,如果梯形与等边三角形的重叠部分的面积是梯形面积的一半,求等边△PMN的边长x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,—抛物线y=﹣a(x+1)(x﹣3)(a>0)与x轴交于A、B两点,与y轴交于点C.抛物线的对称轴与x轴交于点E,过点C作x轴的平行线,与抛物线交于点D,连接DE,延长DE交y轴于点F,连接AD、AF.
(1)点A的坐标为____________,点B的坐标为_________ ;
(2)判断四边形ACDE的形状,并给出证明;
(3)当a为何值时,△ADF是直角三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
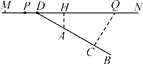
【题目】如图,MN表示一段笔直的高架道路,线段AB表示高架道路旁的一排居民楼,已知点A到MN的距离为15米,BA的延长线与MN相交于点D,且∠BDN=30°,假设汽车在高速道路上行驶时,周围39米以内会受到噪音(XRS)的影响.
(1)过点A作MN的垂线,垂足为点H,如果汽车沿着从M到N的方向在MN上行驶,当汽车到达点P处时,噪音开始影响这一排的居民楼,那么此时汽车与点H的距离为多少米?
(2)降低噪音的一种方法是在高架道路旁安装隔音板,当汽车行驶到点Q时,它与这一排居民楼的距离QC为39米,那么对于这一排居民楼,高架道路旁安装的隔音板至少需要多少米长?(精确到1米)(参考数据:![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行数学竞赛,对获一等奖的学生奖励数学家的著作《好玩的数学》,对获二等奖的学生奖励创意学生笔记本,若网购《好玩的数学》14元/本,创意学生笔记本12元/本,若《好玩的数学》数量比创意学生笔记本的数量的一半多5本,买两种奖品共用了1020元,购买两种奖品的数量各是多少本?

查看答案和解析>>
科目:初中数学 来源: 题型:
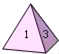
【题目】如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下:
朝下数字 | 1 | 2 | 3 | 4 |
出现的次数 | 16 | 20 | 14 | 10 |
(1)计算上述试验中“4朝下”的频率是 ;
(2)随机投掷正四面体两次,请用列表或画树状图法,求两次朝下的数字之和大于4的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面
的最大距离是5m.
(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如下图)
你选择的方案是_____(填方案一,方案二,或方案三),则B点坐标是______,求出你所选方案中的抛物线的表达式;
(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com