
科目: 来源: 题型:
【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
(1)求∠BCD的度数.
(2)求教学楼的高BD.(结果精确到0.1m,参考数据:tan20°≈0.36,tan18°≈0.32)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=6cm,BC=12cm,∠B=90°.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P,Q分别从A,B同时出发,设移动时间为t(s).

(1)当![]() 时,求△PBQ的面积;
时,求△PBQ的面积;
(2)当![]() 为多少时,四边形APQC的面积最小?最小面积是多少?
为多少时,四边形APQC的面积最小?最小面积是多少?
(3)当![]() 为多少时,△PQB与△ABC相似.
为多少时,△PQB与△ABC相似.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某小型水库栏水坝的横断面是四边形ABCD,DC∥AB,测得迎水坡的坡角α=30°,已知背水坡的坡比为1.2:1,坝顶部DC宽为2m,坝高为6m,则坝底AB的长为_____m.

查看答案和解析>>
科目: 来源: 题型:
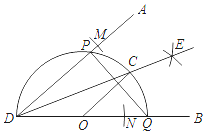
【题目】已知∠ADB,作图.
步骤1:以点D为圆心,适当长为半径画弧,分别交DA、DB于点M、N;再分别以点M、N为圆心,大于![]() MN长为半径画弧交于点E,画射线DE.
MN长为半径画弧交于点E,画射线DE.
步骤2:在DB上任取一点O,以点O为圆心,OD长为半径画半圆,分别交DA、DB、DE于点P、Q、C;
步骤3:连结PQ、OC.
则下列判断:①![]() ;②OC∥DA;③DP=PQ;④OC垂直平分PQ,其中正确的结论有( )
;②OC∥DA;③DP=PQ;④OC垂直平分PQ,其中正确的结论有( )
A. ①③④ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目: 来源: 题型:
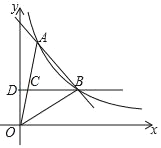
【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y=![]() (a≠0)的图象在第一象限交于A、B两点,A点的坐标为(m,4),B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C.若OC=CA,
(a≠0)的图象在第一象限交于A、B两点,A点的坐标为(m,4),B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C.若OC=CA,
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)在直线BD上是否存在一点E,使得△AOE是直角三角形,求出所有可能的E点坐标.
查看答案和解析>>
科目: 来源: 题型:
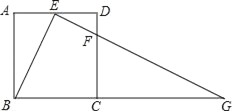
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF:DC=1:4,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为10,求BG的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
①该产品90天售量(n件)与时间(第x天)满足一次函数关系,部分数据如下表:

②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
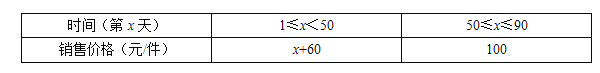
(1)求出第10天日销售量;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品的销售利润最大?最大利润是多少?(提示:每天销售利润=日销售量×(每件销售价格﹣每件成本))
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.
查看答案和解析>>
科目: 来源: 题型:
【题目】规定:身高在选定标准的±2%范围之内都称为“普通身高”.为了解某校九年级男生中具有“普通身高”的人数,我们从该校九年级500名男生中随机选出10名男生,分别测量出他们的身高(单位:cm)收集并整理统计表:

根据以上表格信息,解答如下问题:
(1)计算这组数据的三个统计量:平均数、中位数、众数;
(2)请你选择其中一个统计量作为选定标准,估计该校九年级男生中具有“普通身高”的人数.
查看答案和解析>>
科目: 来源: 题型:
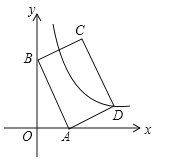
【题目】如图,平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数![]() (x>0)的图像经过点D,则
(x>0)的图像经过点D,则![]() 值为( )
值为( )
A. ﹣14 B. 14 C. 7 D. ﹣7
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△PBD∽△DCA;
(3)当AB=6,AC=8时,求线段PB的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com