
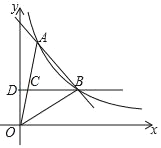
����Ŀ����ͼ��һ�κ���y��kx+b��k��0���뷴��������y��![]() ��a��0����ͼ���ڵ�һ������A��B���㣬A�������Ϊ��m��4����B�������Ϊ��3��2��������OA��OB����B��BD��y�ᣬ����ΪD����OA��C����OC��CA��
��a��0����ͼ���ڵ�һ������A��B���㣬A�������Ϊ��m��4����B�������Ϊ��3��2��������OA��OB����B��BD��y�ᣬ����ΪD����OA��C����OC��CA��
��1����һ�κ����ͷ����������ı���ʽ��
��2�����AOB�������
��3����ֱ��BD���Ƿ����һ��E��ʹ�á�AOE��ֱ�������Σ�������п��ܵ�E�����꣮
���𰸡���1��y��![]() ��y����
��y����![]() x+6����2��
x+6����2��![]() ����3��E��������
����3��E��������![]() ��2����
��2����![]() ��2����
��2����![]() ��2����
��2����![]() ��2����
��2����
��������
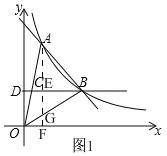
��1�������ô���ϵ���������������������ʽ������ȷ������A�����꣬���ô���ϵ�������һ�κ�������ʽ��
��2������A��AF��x����F��OB��G�������OB�Ľ���ʽ���������AG���������ε������ʽ���ɵó����ۣ�
��3�����������ηֱ�������⼴�ɽ�����⣻
�⣺��1���ߵ�B��3��2���ڷ���������y��![]() ��ͼ���ϣ�
��ͼ���ϣ�
��a��3��2��6��
�෴���������ı���ʽΪy��![]() ��
��
�ߵ�A��������Ϊ4��
�ߵ�A�ڷ���������y��![]() ͼ���ϣ�
ͼ���ϣ�
��A��![]() ��4����
��4����
��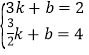 ����
����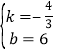 ��
��
��һ�κ����ı���ʽΪy����![]() x+6��
x+6��
��2����ͼ1������A��AF��x����F��OB��G��
��B��3��2����
��ֱ��OB�Ľ���ʽΪy��![]() x��
x��
��G��![]() ��1����
��1����
A��![]() ��4����
��4����
��AG��4��1��3��
��S��AOB��S��AOG+S��ABG��![]() ��3��3��
��3��3��![]() ��
��
��3����ͼ2�У�
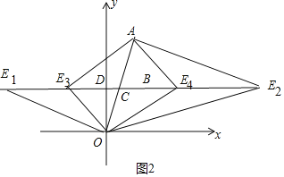
����AOE1��90��ʱ����ֱ��AC�Ľ���ʽΪy��![]() x��
x��
��ֱ��OE1�Ľ���ʽΪy����![]() x��
x��
��y��2ʱ��x����![]() ��
��
��E1����![]() ��2����
��2����
����OAE2��90��ʱ��
ֱ��OE1ƽ��ֱ��OE2
��ֱ��OE2�Ľ���ʽΪy����![]() x+b��
x+b��
��ֱ�߹���A��![]() ��4������b=
��4������b=![]()
��ֱ��OE2�Ľ���ʽΪy����![]() x+
x+![]() ��
��
��y��2ʱ��x��![]() ��
��
��E2��![]() ��2����
��2����
����OEA��90��ʱ��
��A��![]() ��4������OA=
��4������OA=![]()
��AC��OC��CE��![]() ��
��
��C��![]() ��2����
��2����
��ɵ�E3��![]() ��2����E4��
��2����E4��![]() ��2����
��2����
�������������������ĵ�E����Ϊ����![]() ��2����
��2����![]() ��2����
��2����![]() ��2����
��2����![]() ��2����
��2����


 �������ϵ�д�
�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
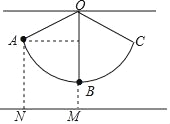
����Ŀ����ͼ����ϸ������һ��С��С������ֱƽ���ڵ�A��C��������ذڶ���A����������AN=14cm��С������͵�Bʱ����������BM=5cm����AOB=66������ϸ��OB�ij��ȣ����ο����ݣ�sin66���0.91��cos66���0.40��tan66���2.25��
���𰸡�15cm
��������
������ϸ��OB�ij���Ϊxcm����AD��OB��D��֤���ı���ANMD�Ǿ��Σ��ó�AN=DM=14cm�����OD=x-9����Rt��AOD�У������Ǻ����ó����̣��ⷽ�̼��ɣ�
�����������ϸ��OB�ij���Ϊxcm����AD��OB��D����ͼ��ʾ��
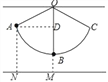
���ADM=90�㣬
�ߡ�ANM=��DMN=90�㣬
���ı���ANMD�Ǿ��Σ�
��AN=DM=14cm��
��DB=14��5=9cm��
��OD=x��9��
��Rt��AOD��cos��AOD=![]() ��
��
��cos66��=![]() =0.40��
=0.40��
��ã�x=15��
��OB=15cm��
�����͡������
��������
20
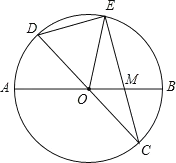
����Ŀ����֪����ͼ���ڰ뾶Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ������ֱ����
������ֱ����![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() ���ӳ��߽�
���ӳ��߽�![]() �ڵ�
�ڵ�![]() ����
����![]() ������
������![]() ��
��![]() .
.
��1����֤��![]() ;
;
��2����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ������������ĩ��λ��ȥ�����ĩ��λ�������µ�����7���IJ��ܱ�19��������������ܱ�19�����������ܱ�19�������ܱ�19���������dz�֮Ϊ������������
��46379����![]() ��
��![]() �ܱ�19������
�ܱ�19������![]() �ܱ�19��������������������
�ܱ�19��������������������
![]() �������������ж�52478��9115�Ƿ�Ϊ������������
�������������ж�52478��9115�Ƿ�Ϊ������������
![]() ��һ����λ������1����λ�����������ĸ�λ���ֲ�Ϊ0����ǧλ���ֵ�2����ʮλ�Ͱ�λ�ϵ�����֮��Ϊ8���������ǡ����������������������������
��һ����λ������1����λ�����������ĸ�λ���ֲ�Ϊ0����ǧλ���ֵ�2����ʮλ�Ͱ�λ�ϵ�����֮��Ϊ8���������ǡ����������������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ľߵ깺��һ������ᣬÿ������Ϊ20Ԫ������Ӫ�����ǣ�Ҫ��ÿ���������ۼ۲�����20Ԫ�Ҳ�����28Ԫ�������۹����з��ָü����ÿ�ܵ�������y��������ÿ���������ۼ�x��Ԫ��֮������һ�κ�����ϵ�������۵���Ϊ22Ԫʱ��������Ϊ36���������۵���Ϊ24Ԫʱ��������Ϊ32����
��1�����y��x�ĺ�����ϵʽ��
��2�����ľߵ�ÿ���������ּ������150Ԫ������ʱ��ÿ�����������۵����Ƕ���Ԫ��
��3������ľߵ�ÿ���������ּ��������õ�����ΪwԪ�����ü�������۵��۶�Ϊ����Ԫʱ������ʹ�ľߵ����۸ü�����������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O����ABC�����Բ��O����BC���ϣ���BAC��ƽ���߽���O�ڵ�D������BD��CD������D��BC��ƽ���ߣ���AB���ӳ����ཻ�ڵ�P��
��1����֤��PD�ǡ�O�����ߣ�
��2����֤����PBD�ס�DCA��
��3����AB=6��AC=8ʱ�����߶�PB�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������˽�����ë���������ë����е�·��Ϊ�����ߵ�һ���֣���ͼ������![]() ��������
��������![]() ��
��![]() ������һ����ë����еĸ߶�
������һ����ë����еĸ߶�![]() ��ˮƽ����
��ˮƽ����![]() ֮�����㺯������ʽ
֮�����㺯������ʽ![]() ����֪��
����֪��![]() ��������ˮƽ����Ϊ
��������ˮƽ����Ϊ![]() �������ĸ߶�Ϊ
�������ĸ߶�Ϊ![]() ��
��
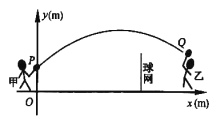
��1����![]() ʱ������
ʱ������![]() ��ֵ����ͨ�������жϴ����ܷ������
��ֵ����ͨ�������жϴ����ܷ������
��2���������������ë����е���![]() ��ˮƽ����Ϊ
��ˮƽ����Ϊ![]() �������ĸ߶�Ϊ
�������ĸ߶�Ϊ![]() ��
��![]() ��ʱ���ҿ���ɹ�����
��ʱ���ҿ���ɹ�����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬�ı���OABC�Ǿ��Σ�OA��x��ĸ������ϣ�OC��y����������ϣ�
![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��ͼ1��������OABC�Ƶ�O˳ʱ�뷽����ת
��ͼ1��������OABC�Ƶ�O˳ʱ�뷽����ת![]() �õ�����
�õ�����![]() ������A�Ķ�Ӧ��
������A�Ķ�Ӧ��![]() ����BC����ʱ�����
����BC����ʱ�����![]() �����ꣻ
�����ꣻ
![]() ��ͼ��������OABC�Ƶ�O˳ʱ�뷽����
��ͼ��������OABC�Ƶ�O˳ʱ�뷽����![]() �õ�����
�õ�����![]() ������B�Ķ�Ӧ��
������B�Ķ�Ӧ��![]() ���������������ʱ�����
���������������ʱ�����![]() �����ꣻ
�����ꣻ
![]() ��
��![]() ��
��![]() ��
��![]() ����ͼ3�����
����ͼ3�����![]() ��BC���ڵ�E����
��BC���ڵ�E����![]() ����ֱ��д��
����ֱ��д��![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ʾ����һ���߳�Ϊ2��������ABCD��һ����Ϊ2����Ϊ1�ľ���CEFDƴ��һ�𣬹���һ����ľ���ABEF���ֽ�С����CEFD�Ƶ�C˳ʱ����ת��CE��F��D�䣬��ת��Ϊ����
��1������D��ǡ������EF����ʱ������ת������ֵ��
��2����ͼ2��GΪBC�е㣬��0�㣼����90�㣬��֤��GD�䣽E��D��
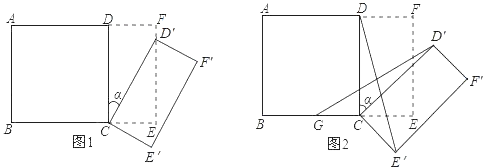
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ijһ�����������¶��壺������ʵ��p�������Ա�����ֵΪpʱ���亯��ֵ����p,���pΪ��������IJ���ֵ.�ں������ڲ���ֵʱ,�ú��������ֵ����С����ֵ֮��q��Ϊ��������IJ��䳤��.�ر��,������ֻ��һ������ֵʱ,�䲻�䳤��qΪ��.���磺��ͼ�еĺ�����0,1��������ֵ,�䲻�䳤��q����1.
(1)�ֱ��жϺ���y=x-1��y=x-1,y=x2��û�в���ֵ������У�ֱ��д���䲻�䳤�ȣ�
(2)����y=2x2-bx.
�����䲻�䳤��Ϊ�㣬��b��ֵ��
����1��b��3,���䲻�䳤��q��ȡֵ��Χ��
(3) �Ǻ���y=x2-2x(x��m)��ͼ��ΪG1����G1��x=m���ۺ�õ��ĺ���ͼ���ΪG2������G��ͼ����G1��G2��������ɣ����䲻�䳤��q����0��q��3,��m��ȡֵ��ΧΪ .
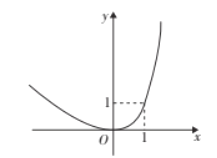
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com