
科目: 来源: 题型:
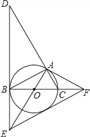
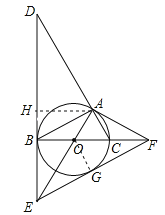
【题目】如图,⊙O是△ABC的外接圆,BC是⊙O的直径,∠ABC=30°,过点B作⊙O的切线BD,与CA的延长线交于点D,与半径AO的延长线交于点E,过点A作⊙O的切线AF,与直径BC的延长线交于点F.
(1)求证:△ACF∽△DAE;
(2)若S△AOC=![]() ,求DE的长;
,求DE的长;
(3)连接EF,求证:EF是⊙O的切线.
【答案】(1) 见解析; (2)3![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:(1)根据圆周角定理得到∠BAC=90°,根据三角形的内角和得到∠ACB=60°根据切线的性质得到∠OAF=90°,∠DBC=90°,于是得到∠D=∠AFC=30°由相似三角形的判定定理即可得到结论;
(2)根据S△AOC=![]() ,得到S△ACF=
,得到S△ACF=![]() ,通过△ACF∽△DAE,求得S△DAE=
,通过△ACF∽△DAE,求得S△DAE=![]() ,过A作AH⊥DE于H,解直角三角形得到AH=
,过A作AH⊥DE于H,解直角三角形得到AH=![]() DH=
DH=![]() DE,由三角形的面积公式列方程即可得到结论;
DE,由三角形的面积公式列方程即可得到结论;
(3)根据全等三角形的性质得到OE=OF,根据等腰三角形的性质得到∠OFG=![]() (180°﹣∠EOF)=30°,于是得到∠AFO=∠GFO,过O作OG⊥EF于G,根据全等三角形的性质得到OG=OA,即可得到结论.
(180°﹣∠EOF)=30°,于是得到∠AFO=∠GFO,过O作OG⊥EF于G,根据全等三角形的性质得到OG=OA,即可得到结论.
试题解析:(1)证明:∵BC是⊙O的直径,∴∠BAC=90°,∵∠ABC=30°,∴∠ACB=60°
∵OA=OC,∴∠AOC=60°,∵AF是⊙O的切线,∴∠OAF=90°,∴∠AFC=30°,∵DE是⊙O的切线,∴∠DBC=90°,∴∠D=∠AFC=30,∵∠DAE=ACF=120°,∴△ACF∽△DAE;
(2)∵∠ACO=∠AFC+∠CAF=30°+∠CAF=60°,∴∠CAF=30°,∴∠CAF=∠AFC,∴AC=CF,∴OC=CF,∵S△AOC=![]() ,∴S△ACF=
,∴S△ACF=![]() ,∵∠ABC=∠AFC=30°,∴AB=AF,∵AB=
,∵∠ABC=∠AFC=30°,∴AB=AF,∵AB=![]() BD,∴AF=
BD,∴AF=![]() BD,∴∠BAE=∠BEA=30°,∴AB=BE=AF,∴
BD,∴∠BAE=∠BEA=30°,∴AB=BE=AF,∴![]() ,∵△ACF∽△DAE,∴
,∵△ACF∽△DAE,∴![]() =
=![]() ,∴S△DAE=
,∴S△DAE=![]() ,过A作AH⊥DE于H,∴AH=
,过A作AH⊥DE于H,∴AH=![]() DH=
DH=![]() DE,∴S△ADE=
DE,∴S△ADE=![]() DEAH=
DEAH=![]() ×
×![]()
![]() =
=![]() ,∴DE=
,∴DE=![]() ;
;
(3)∵∠EOF=∠AOB=120°,∴∠OEB=∠AFO,在△AOF与△BOE中,∵∠OBE=∠OAF,∠OEB=∠AFO,OA=OB,∴△AOF≌△BEO,∴OE=OF,∴∠OFG=![]() (180°﹣∠EOF)=30°,∴∠AFO=∠GFO,过O作OG⊥EF于G,∴∠OAF=∠OGF=90°,在△AOF与△OGF中,∵∠OAF=∠OGF,∠AFO=∠GFO,OF=OF,∴△AOF≌△GOF,∴OG=OA,∴EF是⊙O的切线.
(180°﹣∠EOF)=30°,∴∠AFO=∠GFO,过O作OG⊥EF于G,∴∠OAF=∠OGF=90°,在△AOF与△OGF中,∵∠OAF=∠OGF,∠AFO=∠GFO,OF=OF,∴△AOF≌△GOF,∴OG=OA,∴EF是⊙O的切线.
【题型】解答题
【结束】
25
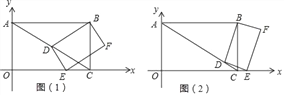
【题目】如图,在平面直角坐标系中,O为原点,四边形ABCO是矩形,点A,C的坐标分别是A(0,2)和C(2![]() ,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF.
,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF.
(1)填空:点B的坐标为 ;
(2)是否存在这样的点D,使得△DEC是等腰三角形?若存在,请求出AD的长度;若不存在,请说明理由;
(3)①求证:![]() ;
;
②设AD=x,矩形BDEF的面积为y,求y关于x的函数关系式(可利用①的结论),并求出y的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】综合实践课上,某小组同学将直角三角形纸片放到横线纸上(所有横线都平行,且相邻两条平行线的距离为1),使直角三角形纸片的顶点恰巧在横线上,发现这样能求出三角形的边长.
(1)如图1,已知等腰直角三角形纸片△ABC,∠ACB=90°,AC=BC,同学们通过构造直角三角形的办法求出三角形三边的长,则AB=__________;

(2)如图2,已知直角三角形纸片△DEF,∠DEF=90°,EF=2DE,求出DF的长;

(3)在(2)的条件下,若橫格纸上过点E的横线与DF相交于点G,直接写出EG的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,关于x的方程a(1﹣x2)+2bx+c(1+x2)=0有两个相等实根,且3c=a+3b
(1)试判断△ABC的形状;
(2)求sinA+sinB的值.
查看答案和解析>>
科目: 来源: 题型:
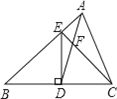
【题目】已知:如图,在△ABC中,D是BC边上的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD;
(2)若S△FCD=5,BC=10,求DE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,小王在长江边某瞭望台D处测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为多少米?(结果精确到0.1,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
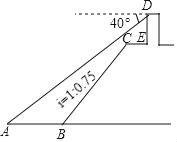
查看答案和解析>>
科目: 来源: 题型:
【题目】全面两孩政策实施后,甲,乙两个家庭有了各自的规划.假定生男生女的概率相同,回答下列问题:
(1)甲家庭已有一个男孩,准备再生一个孩子,则第二个孩子是女孩的概率是 ;
(2)乙家庭没有孩子,准备生两个孩子,求至少有一个孩子是女孩的概率.
查看答案和解析>>
科目: 来源: 题型:
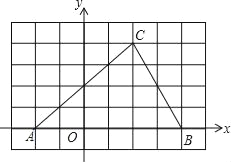
【题目】如图,在6×8的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.
(1)以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′与△ABC位似,且位似比为1:2;(保留作图痕迹,不要求写作法和证明)
(2)若点C的坐标为(2,4),则点A′的坐标为( , ),点C′的坐标为( , ),S△A′B′C′:S△ABC= .
查看答案和解析>>
科目: 来源: 题型:
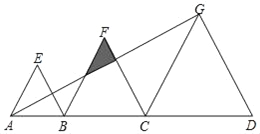
【题目】如图,点B、C是线段AD上的点,△ABE、△BCF、△CDG都是等边三角形,且AB=4,BC=6,已知△ABE与△CDG的相似比为2:5.则
①CD=____;
②图中阴影部分面积为_____.
查看答案和解析>>
科目: 来源: 题型:
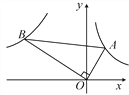
【题目】如图,已知第一象限内的点A在反比例函数y=![]() 的图象上,第二象限内的点B在反比例函数y=
的图象上,第二象限内的点B在反比例函数y=![]() 的图象上,且OA⊥OB,cosA=
的图象上,且OA⊥OB,cosA=![]() ,则k的值为( )
,则k的值为( )
A. -3 B. -4 C. -![]() D. -2
D. -2![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】有这样一个问题:探究同一坐标系中系数互为倒数的正、反比例函数![]() 与
与![]() 的图象性质
的图象性质![]() 小明根据学习函数的经验,对这两个函数当
小明根据学习函数的经验,对这两个函数当![]() 时的图象性质进行了探究
时的图象性质进行了探究![]() 设函数
设函数![]() 与
与![]() 图象的交点为A、
图象的交点为A、![]() 下面是小明的探究过程:
下面是小明的探究过程:
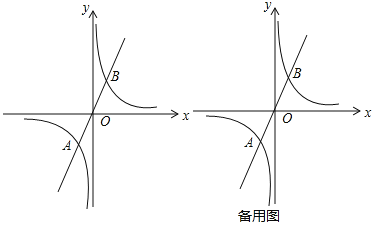
(1)如图所示,若已知A的坐标为![]() ,则B点的坐标为______.
,则B点的坐标为______.
(2)若A的坐标为![]() ,P点为第一象限内双曲线上不同于点B的任意一点.
,P点为第一象限内双曲线上不同于点B的任意一点.
①设直线PA交x轴于点M,直线PB交x轴于点![]() 求证:
求证:![]() .
.
证明过程如下:设![]() ,直线PA的解析式为
,直线PA的解析式为![]() .
.
则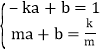
解得![]()
所以,直线PA的解析式为______.
请把上面的解答过程补充完整,并完成剩余的证明.
②当P点坐标为![]() 时,判断
时,判断![]() 的形状,并用k表示出
的形状,并用k表示出![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com