
科目: 来源: 题型:
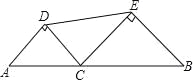
【题目】如图,线段 AB 的长为 4,C 为 AB 上一个动点,分别以 AC、BC 为斜边在 AB 的同侧作两个等腰直角三角形 ACD 和 BCE, 连结 DE, 则 DE 长的最小值是( )
A. ![]() B. 2C.
B. 2C. ![]() D. 4
D. 4
查看答案和解析>>
科目: 来源: 题型:
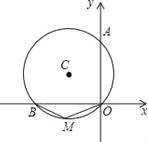
【题目】如图,⊙C 经过原点且与两坐标轴分别交于点 A 与点 B,点 B 的坐标为 ![]() ,M 是圆上一点,∠BMO=120°.⊙C的圆心C的坐标是( )
,M 是圆上一点,∠BMO=120°.⊙C的圆心C的坐标是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
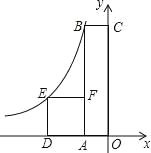
【题目】如图,四边形OABC是矩形,四边形ADEF是正方形,点A、D在x轴的负半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=![]() (k为常数,k≠0)的图象上,正方形ADEF的面积为4,且BF=2AF,则k值为( )
(k为常数,k≠0)的图象上,正方形ADEF的面积为4,且BF=2AF,则k值为( )
A. 4B. -4C. 6D. -6
查看答案和解析>>
科目: 来源: 题型:
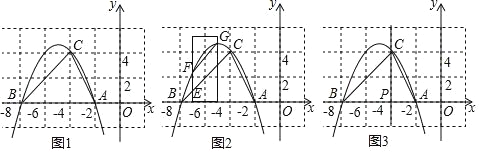
【题目】如图1,抛物线y=﹣![]() x2+bx+c经过点A(﹣2,0),B(﹣8,0),C(﹣4,4).
x2+bx+c经过点A(﹣2,0),B(﹣8,0),C(﹣4,4).
(1)求这个抛物线的表达式;
(2)如图2,一把宽为2的直尺的右边缘靠在直线x=﹣4上,当直尺向左平移过程中刻度线0始终在x轴上,直尺的右边边缘与抛物线和直线BC分别交于G、D点,直尺的左边边缘与抛物线和直线BC分别交于F、E点,当图中四边形DEFG是平行四边形时,此时直尺左边边缘与直线BC的交点E的刻度是多少?
(3)如图3,在直线x=﹣4上找一点K,使得∠ACP+∠AKC=∠ABC(直线x=﹣4与x轴交于P点),请直接写出K点的坐标.
查看答案和解析>>
科目: 来源: 题型:
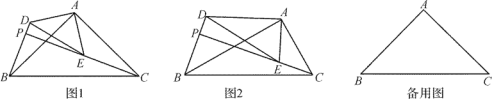
【题目】△ABC和△ADE是有公共顶点的三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
(1) ①如图1,∠ADE=∠ABC=45°,求证:∠ABD=∠ACE.
②如图2,∠ADE=∠ABC=30°,①中的结论是否成立?请说明理由.
(2)在(1) ①的条件下,AB=6,AD=4,若把△ADE绕点A旋转,当∠EAC=90°时,画图并求PB的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】某文具店经销甲、乙两种不同的笔记本.已知:两种笔记本的进价之和为10元,甲种笔记本每本获利2元,乙种笔记本每本获利1元,马阳光同学买4本甲种笔记本和3本乙种笔记本共用了47元.
(1)甲、乙两种笔记本的进价分别是多少元?
(2)该文具店购入这两种笔记本共60本,花费不超过296元,则购买甲种笔记本多少本时该文具店获利最大?
(3)店主经统计发现平均每天可售出甲种笔记本350本和乙种笔记本150本.如果甲种笔记本的售价每提高1元,则每天将少售出50本甲种笔记本;如果乙种笔记本的售价每提高1元,则每天少售出40本乙种笔记本,为使每天获取的利润更多,店主决定把两种笔记本的价格都提高![]() 元,在不考虑其他因素的条件下,当
元,在不考虑其他因素的条件下,当![]() 定为多少元时,才能使该文具店每天销售甲、乙两种笔记本获取的利润最大?
定为多少元时,才能使该文具店每天销售甲、乙两种笔记本获取的利润最大?
查看答案和解析>>
科目: 来源: 题型:
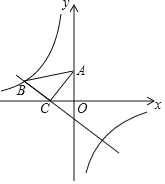
【题目】如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C坐标为(﹣1,0),点A的坐标为(0,2).一次函数y=kx+b的图象经过点B,C,反比例函数y=![]() 的图象也经过点B.
的图象也经过点B.
(1)求反比例函数的关系式;
(2)直接写出当x<0时,kx+b﹣![]() <0的解集.
<0的解集.
查看答案和解析>>
科目: 来源: 题型:
【题目】被誉为“中原第一高楼”的郑州会展宾馆(俗称“大玉米”)坐落在风景如画的如意湖,是来郑州观光的游客留影的最佳景点.学完了三角函数知识后,刘明和王华同学决定用自己学到的知识测量“大王米”的高度,他们制订了测量方案,并利用课余时间完成了实地测量.测量项目及结果如下表:
项目 | 内容 | |||
课题 | 测量郑州会展宾馆的高度 | |||
测量示意图 |
| 如图,在E点用测倾器DE测得楼顶B的仰角是α,前进一段距离到达C点用测倾器CF测得楼顶B的仰角是β,且点A、B、C、D、E、F均在同一竖直平面内 | ||
测量数据 | ∠α的度数 | ∠β的度数 | EC的长度 | 测倾器DE,CF的高度 |
40° | 45° | 53米 | 1.5米 | |
… | … | |||
请你帮助该小组根据上表中的测量数据,求出郑州会展宾馆的高度(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果保留整数)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在等边三角形ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
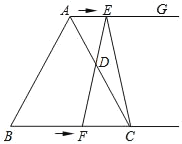
(1)连接EF,当EF经过AC边的中点D时,求证:四边形AFCE是平行四边形;
(2)填空:①当t为 s时,四边形ACFE是菱形;②当t为 s时,△ACE的面积是△ACF的面积的2倍.
查看答案和解析>>
科目: 来源: 题型:
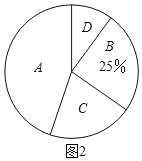
【题目】在创客教育理念的指引下,国内很多学校都纷纷建立创客实践室及创客空间,致力于从小培养孩子的创新精神和创造能力,郑州市某校开设了“3D”打印、数学编程、智能机器人、陶艺制作”四门创客课程,为了解学生对这四门创客课程的喜爱情况,数学兴趣小组对全校学生进行了随机问卷调查(问卷调查表如表所示),将调查结果整理后绘制成图1、图2两幅均不完整的统计图表.
图1
创客课程 | 频数 | 频率 |
A | 36 | 0.45 |
B | 0.25 | |
C | 16 | b |
D | 8 | |
合计 | a | 1 |
最受欢理的创客课程词查问卷
你好!这是一份关于你喜欢的创客深程问卷调查表,请你在表格中选择一个(只能选择一个)你最喜欢的课程选项在其后空格内打“√“,非常感谢你的合作.
选项 | 创客课程 | |
A | “3D”打印 | |
B | 数学编程 | |
C | 智能机器人 | |
D | 陶艺制作 |
请根据图表中提供的值息回答下列问题:
(1)统计表中的a= .b= ;
(2)“D”对应扇形的圆心角为 ;
(3)根据调查结果,请你估计该校2000名学生中最喜欢“数学编程”创客课程的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com