
科目: 来源: 题型:
【题目】(探究)(1)观察下列算式,并完成填空:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
……
![]() .(
.(![]() 是正整数)
是正整数)
(2)某市一广场用正六边形、正方形和正三角形地板砖铺设图案,图案中央是一块正六边形地板砖,周围是正方形和正三角形的地板砖,从里向外第一层包括6块正方形和6块正三角形地板砖;第二层包括6块正方形和18块正三角形地板砖;以此递推.
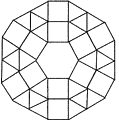
①第3层中分别含有______块正方形和______块正三角形地板砖;
②第![]() 层中含有______块正三角形地板砖(用含
层中含有______块正三角形地板砖(用含![]() 的代数式表示).
的代数式表示).
(应用)
该市打算在一个新建广场中央,也采用这个样式的图案铺设地面,现有1块正六边形、150块正方形和420块正三角形地板砖,问:铺设这样的图案,最多能铺多少层?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】为在中小学生中普及交通法规常识,倡导安全出行,某市教育局在全市范围内组织七年级学生进行了一次“交规记心间”知识竞赛.为了解市七年级学生的竞赛成绩,随机抽取了若干名学生的竞赛成绩(成绩为整数,满分100分),进行统计后,绘制出如下频数分布表和图所示的频数分布直方图(频数分布直方图中有一处错误).
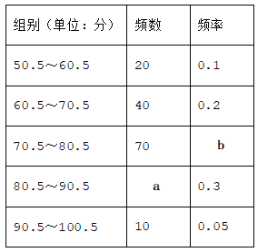
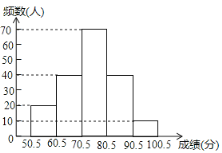
请根据图表信息回答下列问题:
(1)在频数分布表中,![]() ,
,![]() .
.
(2)指出频数分布直方图中的错误,并在上改正;
(3)甲同学说:“我的成绩是此次抽样调查所得数据的中位数”,问:甲同学的成绩应在什么范围?
(4)全市共有5000名七年级学生,若规定成绩在80分以上(不含80分)为优秀,估计这次竞赛中成绩为优秀的学生有多少人?
查看答案和解析>>
科目: 来源: 题型:
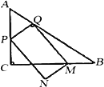
【题目】如图,在锐角![]() 中,延长
中,延长![]() 到点
到点![]() ,点
,点![]() 是
是![]() 边上的一个动点,过点
边上的一个动点,过点![]() 作直线
作直线![]() ,
,![]() 分别交
分别交![]() 、
、![]() 的平分线于
的平分线于![]() ,
,![]() 两点,连接
两点,连接![]() 、
、![]() .在下列结论中.①
.在下列结论中.①![]() ;②
;②![]() ;③若
;③若![]() ,
,![]() ,则
,则![]() 的长为6;④当
的长为6;④当![]() 时,四边形
时,四边形![]() 是矩形.其中正确的是( )
是矩形.其中正确的是( )

A. ①④B. ①②C. ①②③D. ②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】在多项式的乘法公式中,完全平方公式![]() 是其中重要的一个.
是其中重要的一个.
(1)请补全完全平方公式的推导过程:
![]() ,
,
![]() ,
,
![]() .
.
(2)如图,将边长为![]() 的正方形分割成Ⅰ、Ⅱ、Ⅲ、Ⅳ四部分,请你结合图给出完全平方公式的几何解释.
的正方形分割成Ⅰ、Ⅱ、Ⅲ、Ⅳ四部分,请你结合图给出完全平方公式的几何解释.
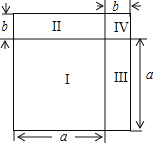
(3)用完全平方公式求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】有两个函数![]() 和
和![]() ,若对于每个使函数有意义的实数
,若对于每个使函数有意义的实数![]() ,函数
,函数![]() 的值为两个函数值中中较小的数,则称函数
的值为两个函数值中中较小的数,则称函数![]() 为这两个函数
为这两个函数![]() 、
、![]() 的较小值函数。例如:
的较小值函数。例如:![]() ,
,![]() ,则
,则![]() 、
、![]() 的较小值函数
的较小值函数![]()
(1)函数![]() 是函数
是函数![]() ,
,![]() 的较小值函数;
的较小值函数;
①在如图的平面直角坐标系中画出函数![]() 的图像.
的图像.
②写出函数![]() 的两条性质.
的两条性质.
(2)函数![]() 是函数
是函数![]() ,
,![]() 的较小值函数,当
的较小值函数,当![]() 时,函数值
时,函数值![]() 的取值范围为
的取值范围为![]() .当
.当![]() 取某个范围内的任意值时,
取某个范围内的任意值时,![]() 为定值.直接写出满足条件的
为定值.直接写出满足条件的![]() 的取值范围及其对应的
的取值范围及其对应的![]() 值.
值.
(3)函数![]() 是函数
是函数![]() ,
,![]() (
(![]() 为常数,且
为常数,且![]() )的较小值函数,当
)的较小值函数,当![]() 时,随着
时,随着![]() 的增大,函数值
的增大,函数值![]() 先增大后减小,直接写出
先增大后减小,直接写出![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 以每秒
以每秒![]() 个单位长度的速度向终点
个单位长度的速度向终点![]() 运动。当点
运动。当点![]() 不与点
不与点![]() 、
、![]() 重合时,在边
重合时,在边![]() 上取一点
上取一点![]() ,满足
,满足![]() ,过点
,过点![]() 作
作![]() ,交边
,交边![]() 于点
于点![]() ,以
,以![]() 、
、![]() 为边做矩形
为边做矩形![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
(1)用含![]() 的代数式表示线段
的代数式表示线段![]() 的长;
的长;
(2)当矩形![]() 为正方形时,求
为正方形时,求![]() 的值;
的值;
(3)设矩形![]() 与
与![]() 重叠部分图形的周长为
重叠部分图形的周长为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(4)作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,作点
,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() .当
.当![]() 、
、![]() 这两点中只有一个点在矩形
这两点中只有一个点在矩形![]() 内部时,直接写出此时
内部时,直接写出此时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】(问题提出)
如图①,在![]() 中,若
中,若![]() ,
,![]() ,求
,求![]() 边上的中线
边上的中线![]() 的取值范围.
的取值范围.
(1)(问题解决)
解决此问题可以用如下方法:延长![]() 到点
到点![]() 使
使![]() ,再连接
,再连接![]() (或将
(或将![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ),把
),把![]() 、
、![]() 、
、![]() 集中在
集中在![]() 中,利用三角形三边的关系即可判断,由此得出中线
中,利用三角形三边的关系即可判断,由此得出中线![]() 的取值范围.
的取值范围.
(2)(应用)
如图②,在![]() 中,
中,![]() 为
为![]() 的中点,已知
的中点,已知![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
(3)(拓展)
如图③,在![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,过点
上,过点![]() 作
作![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() 。已知
。已知![]() ,
,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两车分别从![]() 、
、![]() 两地同时出发,相向而行。甲车中途因故停车一段时间,之后以原速继续行驶到达目的地
两地同时出发,相向而行。甲车中途因故停车一段时间,之后以原速继续行驶到达目的地![]() ,此时乙车同时到达目的地
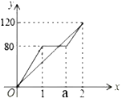
,此时乙车同时到达目的地![]() 。如图,是甲、乙两车离各自的出发地的路程
。如图,是甲、乙两车离各自的出发地的路程![]() 与时间
与时间![]() 的函数图像.
的函数图像.
(1)甲车的速度是多少![]() ,
,![]() 的值为多少;
的值为多少;
(2)求甲车在整个过程中,![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)直接写出甲、乙两车在途中相遇时![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着生活水平的提高,人们对空气质量的要求也越来越高。为了了解![]() 月中旬长春市城区的空气质量情况,某校“综合实践环境调查”小组,从天气预报网抽取了朝阳区和南关区这两个城区
月中旬长春市城区的空气质量情况,某校“综合实践环境调查”小组,从天气预报网抽取了朝阳区和南关区这两个城区![]() 年
年![]() 月
月![]() 日——
日——![]() 年
年![]() 月
月![]() 日的空气质量指数,作为样本进行统计,过程如下,请补充完整.
日的空气质量指数,作为样本进行统计,过程如下,请补充完整.
收集数据
朝阳区 |
|
|
|
|
|
|
|
|
|
|
南关区 |
|
|
|
|
|
|
|
|
|
|
整理、描述数据
按下表整理、描述这两城区空气质量指数的数据.
空气质量 | 优 | 良 | 轻微污染 | 中度污染 | 重度污染 |
朝阳区 | |||||
南关区 |
|
|
|
|
|
(说明:空气质量指数![]() 时,空气质量为优;
时,空气质量为优;![]() 空气质量指数
空气质量指数![]() 时,空气质量为良;
时,空气质量为良;![]() 空气质量指数
空气质量指数![]() 时,空气质量为轻微污染;
时,空气质量为轻微污染;![]() 空气质量指数
空气质量指数![]() 时,空气质量为中度污染;
时,空气质量为中度污染;![]() 空气质量指数
空气质量指数![]() 时,空气质量为重度污染.)
时,空气质量为重度污染.)
分析数据
两城区的空气质量指数的平均数、中位数、方差如下表所示.
城区 | 平均数 | 中位数 | 方差 |
朝阳区 |
|
|
|
南关区 |
|
|
请将以上两个表格补充完整.
得出结论可以推断出哪个城区这十天中空气质量情况比较好?请至少从两个不同的角度说明推断的合理性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com