
科目: 来源: 题型:
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
从上表可知,下列说法正确的有多少个
①抛物线与x轴的一个交点为(﹣2,0);
②抛物线与y轴的交点为(0,6);
③抛物线的对称轴是直线x=![]() ;
;
④抛物线与x轴的另一个交点为(3,0);
⑤在对称轴左侧,y随x增大而减少.
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线![]() 与x轴交于点A、B(点A位于点B左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
与x轴交于点A、B(点A位于点B左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(1)求点A、B、C的坐标;
(2)设动点N(-2,n),求使MN+BN的值最小时n的值;
(3)P是抛物线上位于x轴上方的一点,请探究:是否存在点P,使以P、A、B为顶点的三角形与△ABD相似?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,AC平分∠BCD,AC⊥AB,E是BC的中点,AD⊥AE.
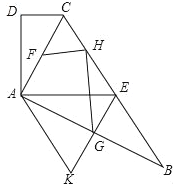
(1)求证:AC2=CD·BC;
(2)过E作EG⊥AB,并延长EG至点K,使EK=EB.
①若点H是点D关于AC的对称点,点F为AC的中点,求证:FH⊥GH;
②若∠B=30°,求证:四边形AKEC是菱形.
查看答案和解析>>
科目: 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B,C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
查看答案和解析>>
科目: 来源: 题型:
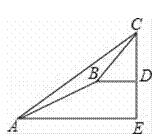
【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,求大树CD的高度?(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)
查看答案和解析>>
科目: 来源: 题型:
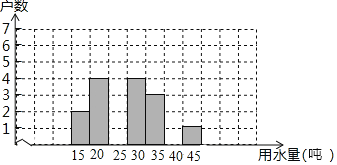
【题目】下表是2018年三月份某居民小区随机抽取20户居民的用水情况::
月用水量/吨 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
户数 | 2 | 4 | m | 4 | 3 | 0 | 1 |
(1)求出m= ,补充画出这20户家庭三月份用电量的条形统计图;
(2)据上表中有关信息,计算或找出下表中的统计量,并将结果填入表中:
统计量名称 | 众数 | 中位数 | 平均数 |
数据 |
|
|
|
(3)为了倡导“节约用水绿色环保”的意识,江赣市自来水公司实行“梯级用水、分类计费”,价格表如下:
月用水梯级标准 | Ⅰ级(30吨以内) | Ⅱ级(超过30吨的部分) |
单价(元/吨) | 2.4 | 4 |
如果该小区有500户家庭,根据以上数据,请估算该小区三月份有多少户家庭在Ⅰ级标准?
(4)按上表收费,如果某用户本月交水费120元,请问该用户本月用水多少吨?
查看答案和解析>>
科目: 来源: 题型:
【题目】为落实“垃圾分类”,环保部门要求垃圾要按A,B,C,D四类分别装袋、投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料、废纸等可回收物,D类指出其他垃圾,小明、小亮各投放了一袋垃圾.
(1)直接写出小明投放的垃圾恰好是A类的概率;
(2)求小亮投放的垃圾与小明投放的垃圾是同一类的概率.
查看答案和解析>>
科目: 来源: 题型:
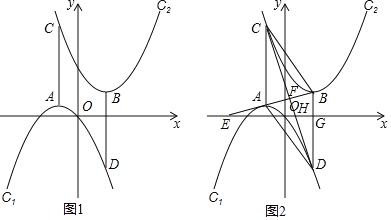
【题目】已知:抛物线C1:y=﹣(x+m)2+m2(m>0),抛物线C2:y=(x﹣n)2+n2(n>0),称抛物线C1,C2互为派对抛物线,例如抛物线C1:y=﹣(x+1)2+1与抛物线C2:y=(x﹣![]() )2+2是派对抛物线,已知派对抛物线C1,C2的顶点分别为A,B,抛物线C1的对称轴交抛物线C2于C,抛物线C2的对称轴交抛物线C1与D.
)2+2是派对抛物线,已知派对抛物线C1,C2的顶点分别为A,B,抛物线C1的对称轴交抛物线C2于C,抛物线C2的对称轴交抛物线C1与D.
(1)已知抛物线①y=﹣x2﹣2x,②y=(x﹣3)2+3,③y=(x﹣![]() )2+2,④y=x2﹣x+
)2+2,④y=x2﹣x+![]() ,则抛物线①②③④中互为派对抛物线的是 (请在横线上填写抛物线的数字序号);
,则抛物线①②③④中互为派对抛物线的是 (请在横线上填写抛物线的数字序号);
(2)如图1,当m=1,n=2时,证明AC=BD;
(3)如图2,连接AB,CD交于点F,延长BA交x轴的负半轴于点E,记BD交x轴于G,CD交x轴于点H,∠BEO=∠BDC.
①求证:四边形ACBD是菱形;
②若已知抛物线C2:y=(x﹣2)2+4,请求出m的值.
查看答案和解析>>
科目: 来源: 题型:
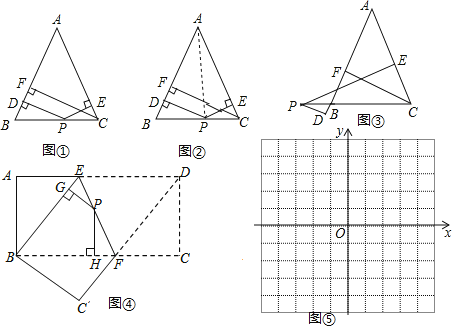
【题目】(问题情境)在△ABC中,AB=AC,点P为BC所在直线上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.当P在BC边上时(如图1),求证:PD+PE=CF.
证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.(不要证明)
(变式探究)(1)当点P在CB延长线上时,其余条件不变(如图3),试探索PD、PE、CF之间的数量关系并说明理由;
请运用上述解答中所积累的经验和方法完成下列两题:
(结论运用)(2)如图4,将长方形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=16,CF=6,求PG+PH的值.
(迁移拓展)(3)在直角坐标系中,直线l1:y=-![]() x+8与直线l2:y=﹣2x+8相交于点A,直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为2.求点P的坐标.
x+8与直线l2:y=﹣2x+8相交于点A,直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为2.求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com