
科目: 来源: 题型:
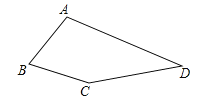
【题目】如图,在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.
(1)求∠A+∠C的度数;
(2)连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由;
(3)若AB=1,点E在四边形ABCD内部运动,且满足AE2=BE2+CE2,求点E运动路径的长度.
查看答案和解析>>
科目: 来源: 题型:
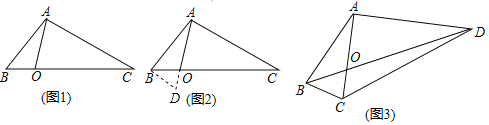
【题目】(1)某学校“智慧方园”数学社团遇到这样一个题目:
如图1,在△ABC中,点O在线段BC上,∠BAO=30°,∠OAC=75°,AO=![]() ,BO:CO=1:3,求AB的长.
,BO:CO=1:3,求AB的长.
经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2).
请回答:∠ADB= °,AB= .
(2)请参考以上解决思路,解决问题:
如图3,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥AD,AO=![]() ,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
查看答案和解析>>
科目: 来源: 题型:
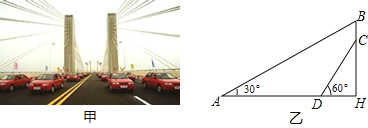
【题目】某大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目: 来源: 题型:
【题目】我国古代伟大的数学家刘微将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形.后人借助这种分割方法所得的图形证明了勾股定理,如图所示若a=3,b=4,则该三角形的面积为( )
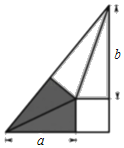
A. 10B. 12C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正△ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿![]() 的方向运动,到达点C时停止,设运动时间为x(秒),
的方向运动,到达点C时停止,设运动时间为x(秒),![]() ,则y关于x的函数的图像大致为( )
,则y关于x的函数的图像大致为( )
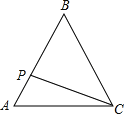
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司投入研发费用40万元(40万元只计入第一年成本),成功研发出一种产品.公司按订单生产(产量=销售量),第一年该产品正式投产后,生产成本为4元/件.此产品年销售量y(万件)与售价x(元件)之间满足函数关系式y=﹣x+20.
(1)求这种产品第一年的利润W(万元)与售价x(元件)满足的函数关系式;
(2)该产品第一年的利润为24万元,那么该产品第一年的售价是多少?
(3)第二年,该公司将第一年的利润24万元(24万元只计入第二年成本)再次投入研发,使产品的生产成本降为3元/件.为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过10万件.请计算该公司第二年的利润W2至少为多少万元.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计,现从该校随机抽取n名学生作为样本,采用问卷调查的方式收集数据![]() 参与问卷调查的每名学生只能选择其中一项
参与问卷调查的每名学生只能选择其中一项![]() ,并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图,由图中提供的信息,解答下列问题:
,并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图,由图中提供的信息,解答下列问题:
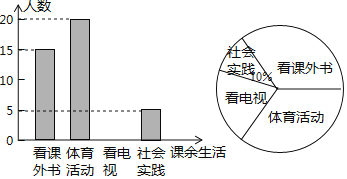
![]() 补全条形统计图;
补全条形统计图;
![]() 若该校共有学生2400名,试估计该校喜爱看电视的学生人数.
若该校共有学生2400名,试估计该校喜爱看电视的学生人数.
![]() 若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名,求恰好抽到2名男生的概率.
若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名,求恰好抽到2名男生的概率.
查看答案和解析>>
科目: 来源: 题型:
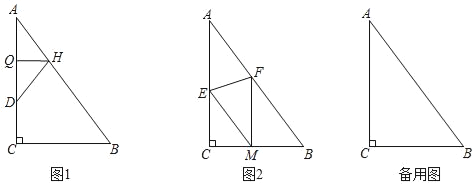
【题目】在△ABC中,∠ACB=90°,AB=25,BC=15.
(1)如图1,折叠△ABC使点A落在AC边上的点D处,折痕交AC、AB分别于Q、H,若S△ABC=9S△DHQ,则HQ= .
(2)如图2,折叠△ABC使点A落在BC边上的点M处,折痕交AC、AB分别于E、F.若FM∥AC,求证:四边形AEMF是菱形;
(3)在(1)(2)的条件下,线段CQ上是否存在点P,使得△CMP和△HQP相似?若存在,求出PQ的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com