
科目: 来源: 题型:
【题目】某小区2号楼对外销售,已知2号楼某单元共33层,一楼为商铺,只租不售,二楼以上价格如下:第16层售价为6000元/米2,从第16层起每上升一层,每平方米的售价提高30元,反之每下降一层,每平方米的售价降低10元,已知该单元每套的面积均为100米2
(1)请在下表中,补充完整售价y(元/米2)与楼层x(x取正整数)之间的函数关系式.
楼层x(层) | 1楼 | 2≤x≤15 | 16楼 | 17≤x≤33 |
售价y(元/米2) | 不售 |
| 6000 |
|
(2)某客户想购买该单元第26层的一套楼房,若他一次性付清购房款,可以参加如图优惠活动.请你帮助他分析哪种优惠方案更合算.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.

(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一架无人机在距离地面高度为13.3米的点A处,测得地面点M的俯角为53°,这架无人机沿仰角为35°的方向飞行了55米到达点B,恰好在地面点N的正上方,M、N在同一水平线上求出M、N两点之间的距离.(结果精确到1米)
(参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33,sin35°≈0.57,cos35°≈0.82,tan35°≈0.70.)

查看答案和解析>>
科目: 来源: 题型:
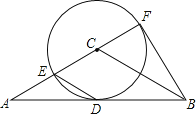
【题目】如图,在△ABC中,AC=BC,AB是⊙C的切线,切点为点D,直线AC交⊙C于点E、F,且CF=![]() AC,
AC,
(1)求证:△ABF是直角三角形.
(2)若AC=6,则直接回答BF的长是多少.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为了解学生对排球、羽毛球、足球、篮球(以下分别用A、B、C、D表示)这四种球类运动的喜好情况.对全体学生进行了抽样调查(每位学生只能选一项最喜欢的运动),并将调查情况绘制成如下两幅不完整的统计图.
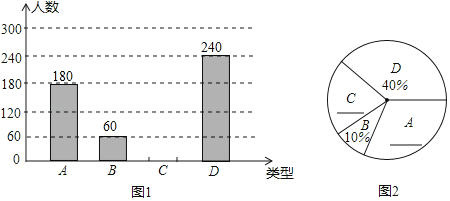
请根据以上信息回答下面问题:
(1)本次参加抽样调查的学生有 人.
(2)补全两幅统计图.
(3)若从本次参加抽样调查的学生中任取1人,则此人喜欢哪类球的概率最大?求其概率.
查看答案和解析>>
科目: 来源: 题型:
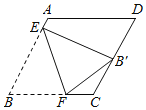
【题目】在菱形ABCD中,AB=2,∠BAD=120°,点E,F分别是边AB,BC边上的动点,沿EF折叠△BEF,使点B的对应点B’始终落在边CD上,则A、E两点之间的最大距离为_____.
查看答案和解析>>
科目: 来源: 题型:
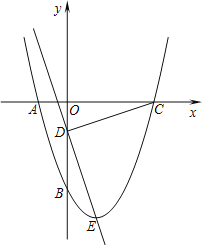
【题目】如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(﹣1,0)、(0,﹣3).
(1)求抛物线的函数解析式;
(2)点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标;
(3)在第二问的条件下,在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,请你直接写出所有满足条件的点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.
(1)求证:直线CE是⊙O的切线.
(2)若BC=3,CD=3![]() ,求弦AD的长.
,求弦AD的长.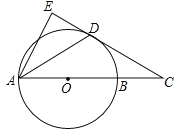
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 年
年![]() 月,振华中学举行了迎国庆中华传统文化节活动.本次文化节共有五个活动:
月,振华中学举行了迎国庆中华传统文化节活动.本次文化节共有五个活动:![]() 书法比赛;
书法比赛;![]() 国画竞技;
国画竞技;![]() 诗歌朗诵;
诗歌朗诵;![]() 汉字大赛;
汉字大赛;![]() 古典乐器演奏.活动结束后,某班数学兴趣小组开展了“我最喜爱的活动”的抽样调查(每人只选一项),根据收集的数据绘制了两幅不完整的统计图,请根据图中信息,解答下列问题:
古典乐器演奏.活动结束后,某班数学兴趣小组开展了“我最喜爱的活动”的抽样调查(每人只选一项),根据收集的数据绘制了两幅不完整的统计图,请根据图中信息,解答下列问题:
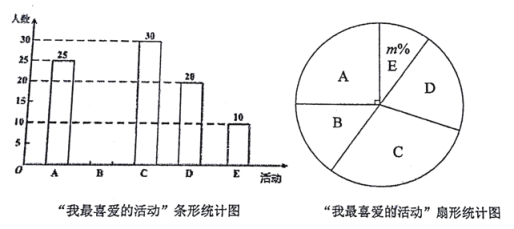
(1)此次催记抽取的初三学生共 人,![]() ,并补全条形统计图;
,并补全条形统计图;
(2)初三年级准备在五名优秀的书法比赛选手中任意选择两人参加学校的最终决赛,这五名选手中有三名男生和两名女生,用树状图或列表法求选出的两名选手正好是一男一女的概率是多少.
查看答案和解析>>
科目: 来源: 题型:
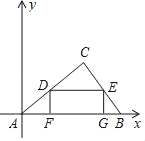
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,以点A为原点建立平面直角坐标系,使AB在x轴正半轴上,点D是AC边上的一个动点,DE∥AB交BC于E,DF⊥AB于F,EG⊥AB于G.以下结论:
①△AFD∽△DCE∽△EGB;
②当D为AC的中点时,△AFD≌△DCE;
③点C的坐标为(3.2,2.4);
④将△ABC沿AC所在的直线翻折到原来的平面,点B的对应点B1的坐标为(1.6,4.8);
⑤矩形DEGF的最大面积为3.在这些结论中正确的有_____(只填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com