
【题目】某小区2号楼对外销售,已知2号楼某单元共33层,一楼为商铺,只租不售,二楼以上价格如下:第16层售价为6000元/米2,从第16层起每上升一层,每平方米的售价提高30元,反之每下降一层,每平方米的售价降低10元,已知该单元每套的面积均为100米2
(1)请在下表中,补充完整售价y(元/米2)与楼层x(x取正整数)之间的函数关系式.
楼层x(层) | 1楼 | 2≤x≤15 | 16楼 | 17≤x≤33 |
售价y(元/米2) | 不售 |
| 6000 |
|
(2)某客户想购买该单元第26层的一套楼房,若他一次性付清购房款,可以参加如图优惠活动.请你帮助他分析哪种优惠方案更合算.

【答案】(1)10x+5840,30x+5520;(2)见解析.
【解析】
(1)根据题意可以分别写出2≤x≤15和17≤x≤33对应的函数解析式,本题得以解决;
(2)根据(1)中的函数关系式可以求得第26层的价格,即可写出两种优惠活动的花费,然后利用分类讨论的方法即可解答本题.
解:(1)由题意可得,
当2≤x≤15时,y=6000﹣(16﹣x)×10=10x+5840,
当17≤x≤33时,y=6000+(x﹣16)×30=30x+5520,
故答案为:10x+5840,30x+5520;
(2)第26层每平方米的价格为:30×26+5520=6300元,
方案一应付款:W1=100×6300×(1﹣5%)﹣m=598500﹣m,
方案二应付款:W2=100×6300×(1﹣7%)=585900,
当W1>W2时,598500﹣m>585900,得m<12600,
当W1=W2时,598500﹣m=585900,得m=12600,
当W1<W2时,598500﹣m>585900,得m>12600,
所以当m<12600时,方案二合算;
当 m=12600时,二个方案相同;
当m>12600时,方案一合算.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
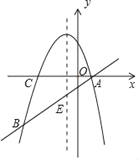
【题目】如图,抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=﹣1,抛物线交x轴于A、C两点,与直线y=x﹣1交于A、B两点,直线AB与抛物线的对称轴交于点E.
(1)求抛物线的解板式.
(2)点P在直线AB上方的抛物线上运动,若△ABP的面积最大,求此时点P的坐标.
(3)在平面直角坐标系中,以点B、E、C、D为顶点的四边形是平行四边形,请直接写出符合条件点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
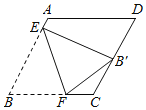
【题目】在菱形ABCD中,AB=2,∠BAD=120°,点E,F分别是边AB,BC边上的动点,沿EF折叠△BEF,使点B的对应点B’始终落在边CD上,则A、E两点之间的最大距离为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
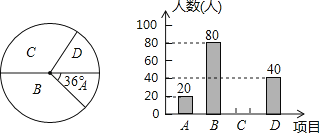
【题目】某学校为了提高学生学科能力,决定开设以下校本课程:A.文学院;B.小小数学家;C.小小外交家;D、未来科学家.为了了解学生最喜欢哪一项校本课程,学校随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次统计共抽查了 名学生;在扇形统计图中,表示C类别的扇形圆心角度数为 .
(2)补全条形统计图;
(3)一班想从表达能力很强的甲、乙、丙、丁四名同学中,任选2名参加小小外交家小组,请用列表或画树状图的方法求恰好同时选中甲、乙两名同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
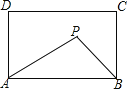
【题目】如图,在矩形ABCD中,AB=4,AD=3,矩形内部有一动点P满足S△PAB=![]() S矩形ABCD,则点P到A、B两点的距离之和PA+PB的最小值为______.
S矩形ABCD,则点P到A、B两点的距离之和PA+PB的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,B的坐标分别为(-4,5),(-2,1).

(1)写出点C及点C关于y轴对称的点C′的坐标;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
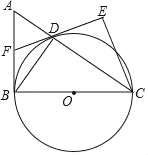
【题目】如图,已知直角△ABC中,∠ABC=90°,BC为圆O的直径,D为圆O与斜边AC的交点,DE为圆O的切线,DE交AB于F,且CE⊥DE.
(1)求证:CA平分∠ECB;
(2)若DE=3,CE=4,求AB的长;
(3)记△BCD的面积为S1,△CDE的面积为S2,若S1:S2=3:2.求sin∠AFD的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com