
科目: 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃,其中一边靠墙,另外三边用长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃垂直于墙的一边长为x米.
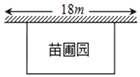
(1)若苗圃的面积为72平方米,求x的值;
(2)这个苗圃的面积能否是120平方米?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 和直线y=(k+1)x+(k+1)2.
和直线y=(k+1)x+(k+1)2.
(1)求证:无论k取何值,抛物线总与x轴有两个不同的交点;
(2)如果抛物线与x轴的交点A,B在原点的右边,直线与x轴的交点C在原点的左边,又抛物线、直线分别交y轴于点D,E,直线AD交直线CE于点G(如图),且CAGE=CGAB,求抛物线的解析式.
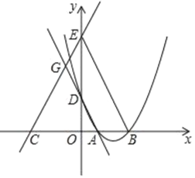
查看答案和解析>>
科目: 来源: 题型:
【题目】一个抛物线形状与二次函数y=x2的图象形状和顶点相同,但开口方向不同.
(1)求抛物线解析式.
(2)如果该抛物线与一次函数y=kx﹣2相交于A、B两点,已知A点的纵坐标为﹣1,求△OAB的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某社区决定把一块长![]() ,宽
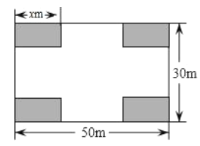
,宽![]() 的矩形空地建成居民健身广场,设计方案如图,阴影区域为绿化区(四块绿化区为大小、形状都相同的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于
的矩形空地建成居民健身广场,设计方案如图,阴影区域为绿化区(四块绿化区为大小、形状都相同的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于![]() ,不大于
,不大于![]() ,设绿化区较长边为
,设绿化区较长边为![]() ,活动区的面积为
,活动区的面积为![]() .为了想知道出口宽度的取值范围,小明同学根据出口宽度不小于
.为了想知道出口宽度的取值范围,小明同学根据出口宽度不小于![]() ,算出
,算出![]() .
.
(1)求![]() 与
与![]() 的函数关系式并直接写出自变量
的函数关系式并直接写出自变量![]() 的取值范围;
的取值范围;
(2)求活动区的最大面积;
(3)预计活动区造价为50元/![]() ,绿化区造价为40元/
,绿化区造价为40元/![]() ,若社区的此项建造投资费用不得超过72000元,求投资费用最少时活动区的出口宽度?
,若社区的此项建造投资费用不得超过72000元,求投资费用最少时活动区的出口宽度?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=-x2+4x+5.
(1)用配方法将y=-x2+4x+5化成y=a(x﹣h)2+k的形式;
(2)指出抛物线的开口方向、对称轴和顶点坐标;
(3)若抛物线上有两点A(x1,y1),B(x2,y2),如果x1>x2>2,试比较y1与y2的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】新定义:[a,b,c]为二次函数y=ax2+bx+e(a≠0,a,b,c为实数)的“图象数”,如:y=-x2+2x+3的“图象数”为[-1,2,3]
(1)二次函数y=![]() x2-x-1的“图象数”为 .
x2-x-1的“图象数”为 .
(2)若图象数”是[m,m+1,m+1]的二次函数的图象与x轴只有一个交点,求m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c(a≠0)与x轴交于点A(﹣1,0)和B(3,0),与y轴交于点C,点D的横坐标为m(0<m<3),连结DC并延长至E,使得CE=CD,连结BE,BC.
(1)求抛物线的解析式;
(2)用含m的代数式表示点E的坐标,并求出点E纵坐标的范围;
(3)求△BCE的面积最大值.

查看答案和解析>>
科目: 来源: 题型:
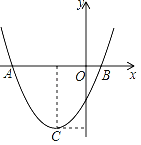
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点C的坐标为(﹣1,﹣3),与x轴交于A(﹣3,0)、B(1,0),根据图象回答下列问题:
(1)写出方程ax2+bx+c=0的根;
(2)写出不等式ax2+bx+c>0的解集;
(3)若方程ax2+bx+c=k有实数根,写出实数k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)如图所示,下列结论中:
①4ac-b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠-1).
其中正确的结论有( )
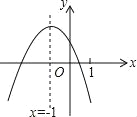
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com