
科目: 来源: 题型:
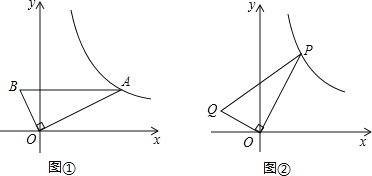
【题目】如图①,直角三角形AOB中,∠AOB=90°,AB平行于x轴,OA=2OB,AB=5,反比例函数的图象经过点A.
(1)直接写出反比例函数的解析式;
(2)如图②,P(x,y)在(1)中的反比例函数图象上,其中1<x<8,连接OP,过O 作OQ⊥OP,且OP=2OQ,连接PQ.设Q坐标为(m,n),其中m<0,n>0,求n与m的函数解析式,并直接写出自变量m的取值范围;
(3)在(2)的条件下,若Q坐标为(m,1),求△POQ的面积.
查看答案和解析>>
科目: 来源: 题型:
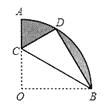
【题目】如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠.点O恰好落在弧AB上点D处,折痕交OA于点C,求整个阴影部分的周长和面积.
查看答案和解析>>
科目: 来源: 题型:
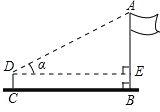
【题目】某校九年级四个数学活动小组参加测量操场旗杆高度的综合实践活动,如图是四个小组在不同位置测量后绘制的示意图,用测角仪测得旗杆顶端A的仰角记为α,CD为测角仪的高,测角仪CD的底部C处与旗杆的底部B处之间的距离记为CB,四个小组测量和计算数据如下表所示:
数据组别 | CD的长(m) | BC的长(m) | 仰角α | AB的长(m) |
第一组 | 1.59 | 13.2 | 32° | 9.8 |
第二组 | 1.58 | 13.4 | 31° | 9.6 |
第三组 | 1.57 | 14.1 | 30° | 9.7 |
第四组 | 1.56 | 15.2 | 28° |
(1)利用第四组学生测量的数据,求旗杆AB的高度(精确到0.1m);
(2)四组学生测量旗杆高度的平均值约为 m(精确到0.1m).
(参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A的坐标为(-2,0),等边三角形AOC经过平移或轴对称或旋转对称都可以得到△OBD。
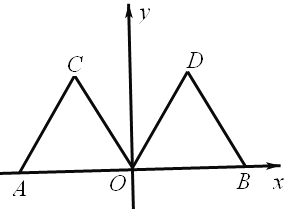
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是 个单位长度;△AOC与△OBD关于直线对称,则对称轴是 ;△AOC绕原点O顺时针旋转得到△OBD,则旋转角可以是 度;
(2)连接AD,交OC于点E,求∠AEO的度数。
查看答案和解析>>
科目: 来源: 题型:
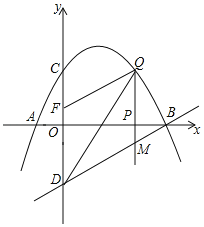
【题目】如图,已知抛物线y=﹣![]() +bx+c的图象经过点A(﹣1,0)和点C(0,2),点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q,交直线BD于点M.
+bx+c的图象经过点A(﹣1,0)和点C(0,2),点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式.
(2)已知点F(0,![]() ),当点P在x轴正半轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
),当点P在x轴正半轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
(3)点P在线段AB运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
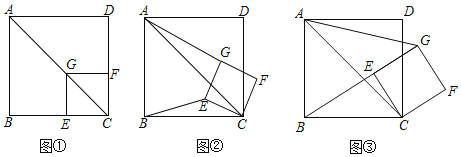
【题目】如图(1),将正方形ABCD与正方形GECF的顶点C重合,当正方形GECF的顶点G在正方形ABCD的对角线AC上时,![]() 的值为______.
的值为______.
如图(2),将正方形CEGF绕点C顺时针方向旋转a角(0°<a<45°),猜测AG与BE之间的数量关系,并说明理由.
如图(3),将正方形CEGF绕点C顺时针方向旋转a角(45°<a<90°)使得B、E、G三点在一条直线上,此时tan∠GAC=![]() ,AG=6,求△BCE的面积.
,AG=6,求△BCE的面积.
查看答案和解析>>
科目: 来源: 题型:
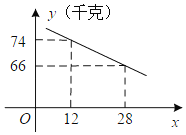
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该果园每棵果树产果y(千克),增种果树x(棵),它们之间的函数关系如图所示.
(1)求y与x之间的函数关系式.
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实7000千克.
(3)当增种果树多少棵时,果园的总产量w(千克)最大?此时每棵果树的产量是多少?
查看答案和解析>>
科目: 来源: 题型:
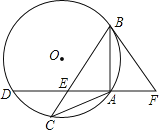
【题目】已知:如图,△ABC内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.
(1)求证:BF与⊙O相切.
(2)若BF=5,cosC=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目: 来源: 题型:
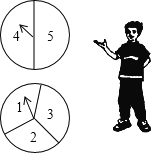
【题目】甲、乙两人用如图所示的两个分格均匀的转盘做游戏:分别转动两个转盘,转盘停止后,指针指向一个数字(若指针恰好停在分格线上,则重转一次),用所指的两个数字求和,如果和大于6,那么甲获胜;如果和不大于6,那么乙获胜.请你帮忙解决下列问题:
(l)利用树状图(或列表)的方法表示游戏所有可能出现的结果.
(2)求甲、乙两人获胜的概率,并说明游戏是否公平.
查看答案和解析>>
科目: 来源: 题型:
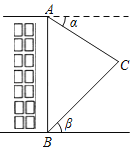
【题目】如图,建筑物AB的高为52米,在其正前方广场上有人进行航模试飞.从建筑物顶端A处测得航模C的俯角α=30°,同一时刻从建筑物的底端B处测得航模C的仰角β=45°,求此时航模C的飞行高度.(精确到1米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45)
≈2.45)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com